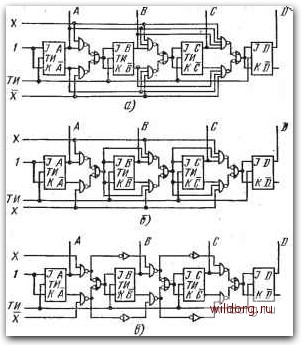Рис. 6.86. Примеры схем реверсивных счетчиков с коэффициентом пересчета 16:

с) с параллельным переносом; б), в) с последовательным переносом

синтез реверсивного счетчика на С-триггерах. Его состояние изменяется при сигналах Z = 1 в последовательности О, 1, 2..... 15,

0, а при сигналах X = 0 - в последовательности О, 15, 14, 13, ....

1, 0. В принципе это объединенные карты суммирующего и вычитающего счетчиков, как это вытекает и из результирующих выражений входов J и К.

Примеры схем демонстрируются на рис. 6.86. На рис. 6.8ба - схема с параллельным переносом.и логическими схемами И-НЕ. Достоинством схемы, является большое быстродействие, а недостатком- возрастающее с числом каскадов счетчика число входов элементов И-НЕ и растущие требования к разветвлению выходов триггеров. На рис. 6.866 показана схема с последовательным переносом. Достоинство схемы заключается в использовании идентичных логических схем после второго каскада. Однако этот счетчик имеет меньшее быстродействие. Следующая схема на рис. 6.86е - это счетчик с последовательным переносом и идентичными элементами И-НЕ, имеющими по два входа, но здесь должны быть использованы инверторы.

Комбинация последовательного и параллельного переносов позволяет получить компромиссные схемы счетчиков, обладающих достаточно высоким быстродействием, причем могут быть использованы элементы с меньшим числом входов, чем в схемах с параллельным переносом. Схема такого счетчика показана на рис. 6.87а. Вместо схем И-НЕ могут быть использованы другие логические эле-

менты. Схема в базисе ИЛИ-НЕ представлена на рис. 6.876. На рис. 6.87в - схема так называемого гибридного счетчика, в котором тактовыми импульсами управляются только первые два каскада счетчика, а другие два работают асинхронно. Схема представляет компромисс между простотой асинхронных счетчиков, которые будут рассмотрены ниже, и быстродействием синхронных счетчиков.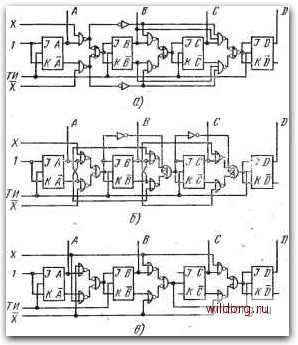

Рис. 6.87., Примеры схем реверсивных счетчиков с коэффициентом пересчета 16: а), б) с последовательно-параллельным переносом; в) гибридный счетчик

На рис. 6.88 приведен пример схемы счетчика на триггерах, управляемых обоими-фронтами тактовых импульсов. /5-триггеры работают в функции /,/С. Счетчик может быть установлен в требуемое состояние соответствующим использованием асинхронных управляющих входов R и S. Схемы на рис. 6.886, в также используют последовательный перенос.

Логика и вся схема может быть значительно упрощена при использовании триггеров с больщйм числом управляющих входов /, К (рнс. 6.89).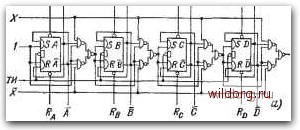

Pmc. Примеры схем реверсивных счетчиков с коэффициентом пересчета 16. Последовательный перенос

ТИ-X-

ьн)л-с

Щ)У D ]

Рис. 6.89. Реверсивный счетчик с 16 состояниями

ч

Десятичные счетчики

Благодаря широкому распространению и возможности использования в логических субсистемах, эти счетчики обычно рассматриваются как специальные. Они получены на основе обычных двоич-