ные на основе соответствующих алгебраических выражений Уь выполняют требуемые функции, но имеют разные свойства. Обратим, например, внимание на случай в на рис. 6.12 с двумя неустойчивыми состояниями при значениях входных сигналов Si? = 11. В этом состоянии схема генерирует. При синтезе всегда стремятся получить наиболее простую схему, отвечающую данным условиям. В данном случае это схема ИЛИ-НЕ на рис. 6.1 Id Как будет показано далее, все остальные возможные схемы являются вариантами основного триггера ИЛИ-НЕ.

В показанном примере была рассмотрена только одна петля

обратной связи tji с выходом Qi=yi. Так как Q2=yi, то дополняющий выход Q2 может быть получен с помощью вспомогательного инвертора (см. рис. 6.11). Если первой строке сокращенной таблицы развития будут соответствовать значения yiy2=0l, а второй строке - значения у±у2- Ю, то состояние выходов QiQz будет соответствовать значениям yiyz, т. е. выходы Qi-yi и Q2=yz-В этом случае необходимы две обратные связи с переменными yi и yz, которые могут иметь четыре комбинации значений 1 и 0. Поэтому карта развития на рис. бЛЗа должна иметь четыре стро-

00 О/ 11 10 СО 01 11 10 00 01 11 10 00 01 11 10

Ш2\ 00

. 10:

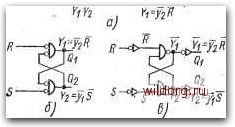Рис. 6.13. Синтез простого 1/?5-триггера с двумя петлями обратной связи:

а) определение функции Yi и Уг; б) схема в базисе ИЛИ-НЕ; б) схема в базисе И-НЕ

КИ, две из которых избыточны. Карту функций У1У2 составим так же, как на рис. 6.11. Устойчивым состояниям 1 и 4 соответствуют значения YiY2=yiyz=0l, устойчивым состояниям 3 и 2 - значения 1112=12=10. Определение значений У1У2, соответствующих неустойчивым состояниям 2 и 4, сложнее, чем на рис. 6.11. Согласно требуемой функции должен происходить переход из неустойчивого состояния 4 в устойчивое состояние 4 и из неустойчивого состояния 2 в устойчивое состояние 2. Этим состояниям можно придать 170

любые значения У1У2, но так, чтобы было выполнено условие УУ2ФУ1У2- С функциональной точки зрения желательны такие значения У1У2, чтобы по возможности не имели место критические последовательности, являющиеся результатом одновременного изменения нескольких внутренних переменных. Такие критические последовательности возникают, например, при одновременном изменении обеих внутренних переменных - у1у2 - в последовательности 00->-11; 11->-00; 01->-10; 10->-01. Следующим условием является самая простая результирующая схема. В карте развития на рис. 6.13а обозначим стрелками все возможные изменения внутренних переменных из неустойчивого состояния 4 в устойчивое 4 и из неустойчивого состояния 2 в устойчивое 2. Из показанных последовательностей вытекает, что значительное упрощение обеспечивают избыточные строки с неспецифицированными состояниями. Если выбрать, например, для неустойчивого состояния 4 зна-, чения У1У2=00, то с точки зрения наиболее простой функции Yi самым целесообразным является изменение внутренних переменных у\У2 в последовательности 10->-00->-01. Из неустойчивого состояния со значениями У1У2=00 наиболее выгодны изменения переменных уху2 в последовательности 01->-00->-10. Этим определены и соответствующие значения У1У2, которые записываются в карту функций У,У2, а из этой карты получают сразу алгебраические выражения отдельных функций У1 и Уг. Для большей наглядности на рис. 6.13а изображены также карты функций У и Уг отдельно. Результирующая схема триггера на элементах ИЛИ-НЕ показана на рис. 6.136, на рис. 6.13в - схема на элементах И-НЕ. Так как в карте развития имеется большое число неспецифицированных состояний, то ясно, что существует много других схем триггеров, отвечающих требуемой функции. >

Запоминающий RS-триггер типа И-НЕ. Согласно рис. 6.14а он состоит из двух элементов - И-НЕ. Из таблицы на рис 6.16 следует зависимость состояния выходов от состояния входов в данный момент, последующая зависимость состояния выходов в момент t+ видна из характеристической таблицы на рис. 6.14в, а программирование входов для обеспечения нормального режима работы без критических состояний показано в таблице функционирования на рис. 6.14г. Временная диаграмма нормального режима работы приведена на рис. 6.145.

От триггера типа ИЛИ-НЕ данный триггер отличается, прежде всего, тем, что при одновременном состоянии входов R=S=0 имеем Qi=,Q2=l. Поэтому для обеспечения функции запоминания в состоянии покоя на обоих входах триггера должны быть значения R=S = l. А из этого вытекает, что активные сигналы, управляющие входами R и S, должны иметь значение 0. Работу этого триггера нельзя словесно сформулировать так же, как работу триггера ИЛИ-НЕ. С точки зрения двойственности обоих триггеров формулировка следующая: триггер устанавливается в активное состояние О сигналом О на входе S и устанавливается в состояние покоя 1. сигналом О на входе R. Однако такая формулировка про-

тиворечит установленным правилам, согласно которым активное состояние триггера имеет всегда значение 1. Это условие выполняется, если принять следующую формулировку: триггер уставав-

Oil)

Puc. 6.14. Запоминающий JS-триггер типа И-НЕ:

a) основная схема; б) зависимость состояния выходов от состояния входов в данный момент t; в) характеристическая таблица; г) таблица функционирования; в) временная диаграмма для нормальных рабочих условий; е) условное обозначение

ливается в активное состояние 1 сигналом О на входе S и устанавливается в состояние покоя О сигналом О на входе R. Согласно такому определению на рис. 6.14а активным будет выход Qi, в отличие от триггера ИЛИ-НЕ, у которого активным является выход Q2.

На практике в схемах часто используются двойственный символ И-НЕ с кружками на входах и символ на рис. 6.14е, у которого кружки на входах R м S должны обозначать различный принцип управления сигналами 0. Создание подходящих несложных символов триггеров довольно трудно, как будет видно уже на этом простом примере. Основным является символ триггера ИЛИ-НЕ, для которого справедливо, что Qi=Q2=0 при R-S=\. Кружки на входах символа означают, в принципе, инверторы перед входами R и S. Если для триггера И-НЕ должен быть справедлив символ на рис, 6.14е, то должно быть Qi = Qa=l при R=S=0. Однако можно легко выяснить, что так же, как у триггера ИЛИ-НЕ, здесь при R = SO состояния выходов Qi=Q2=0, т. е. символ на рис. 6.14е можно считать символом триггера И-НЕ, двойственным символу триггера ИЛИ-НЕ, если у обоих триггеров не принимаются во внимание ненормальные рабочие условия, возникающие при одинаковых состояниях входов R и S. Такой вывод будет получен и при сравнении таблиц переходов обоих триггеров, которые будут одинаковы, если рассматривать в таблице на 172