ОйраМеМный Шд

Wai-

1-j /)

J в к в

J с ВС

j bW km

Вопбинационная логическая суема

Рис. 6.121. а) Простая схема сдвигового регистра с ОС; б) общая схема сдвигового регистра с ОС

На рис. 6.121а приведена для примера очень простая схема с обратными связями с выходов триггера D на входы /, К триггера А. Информация (записанная в регистр с параллельных входов) сдвигается на один разряд вправо после каждого тактового импульса и циркулирует в регистре до тех пор, пока подаются тактовые импульсы. В рассматриваемом случае с простой обратной связью на выходе триггера D последовательно появляются четыре записанных бита, т. е. длина одного цикла L=4. Введением других обратных связей можно получить циклы разной длины. Общая схема сдвигового регистра с обратными связями показана на рис. 6.1216. Обратим внимание, что обратная связь идет с выхода комбинационной логической схемы только к первому каскаду сдвигового регистра. Это упрощает схему, так как для разных длин цикла с выбранным кодом достаточно только определить алгебраическое выражение функции F обратной связи первого каскада регистра, а схема следующих каскадов не меняется. Это, естественно, очень выгодно и с точки зрения практической реализации схемы.

Максимальная величина зависит от числа каскадов п сдвигового регистра и может быть произвольно сокращена. Различные возможности регистра с обратными связями с числом каскадов л=3 на рис. 6.122а. Эта диаграмма заполняется следующим обра-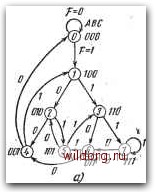

fuc. 6.122. а) Общая диаграмма состояний сдвигового регистра с ОС, имеющего п=з каскадов; б), в) два разных цикла с длиной L=&

ABCD 0000

WOPG

30m. Предположим, что состояние регистра ЛБС=000. Следующее состояние регистра зависит от того, какое значение имеет функция обратной связи, f=0 или F=\. Если lF=iO, то состояние

регистра не меняется. Если if = 1, то следующее состояние регистра АВС= 100 и т. д. Таблицы на рис. дЛ22б, в показывают два разных цикла с длиной L = 8. Из диаграммы состояний видно также, что может существовать несколько циклов разной длины L.

С возрастанием числа каскадов диаграммы состояний становятся все сложнее. В качестве примера на рис. 6.123 приведена диаграмма состояний регистра с ОС с числом каскадов п = 4.

Сдвиговые регистры с обратными связями с длиной цикла L = 2"

Как вытекает из представленных диаграмм состояний, максимальная длина цикла сдвигового регистра с ОС равна L = 2"; число возможных циклов, имеющих такую длину, определяется Л=2(2""

На рис. 6.124с приведен пример одного выбранного цикла трехкас-кадного сдвигового регистра с ОС согласно диаграмме состояний на рис. 6.122. Как показывают приведенные карты, составление схемы регистра очень просто. Если регистр находится в состоянии ЛБС=000, то следующее состояние будет 100 и функция обратной связи F=4. Поэтому в поле, соответствующее состоянию Л5С = 000, запишем F=l. Из состояния ЛБС=100 регистр переключится в состояние ПО; в поле, соответствующее состоянию 100, запишем F=l и т. д.-Так же просто составляется программная карта входов первого триггера регистра. После перехода из состояния ЛБС=000 в состояние 100 триггер Л переключится с О на 1. Если предположить, что использован (-триггер, имеющий программную табл. 6.1, то для этого изменения входы /, К должны иметь значение JK=10, которое записывается в поле Л5С=000, и т. д. Однако в данном случае алгебраические логические соотношения J и К можно определить проще. Логические свойства (-триггера можно выразить характеристическим уравнением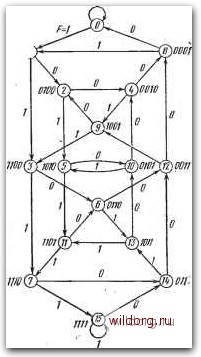

Рис. 6.123. Общая диаграмма состояний четырехкаскадного сдвигового регистра с ОС

(6.9)

Если не производить полной минимизации функции обратной связи и выразить ее в виде

F=A {БС+ВС)+АС, то из сравнения ур-ний (6.9) и (6.10) вытекает, что - Jr,=BC+BC; Кп=С.

(6.10)

00 01 10 10

1

F=fiC+BC-fiBC

w!uFAC-m-m=M+A(Bcm)

A 00 BI 11 10

Jf=BC+BC

A 00 01 11 10

FBCMABC или F=A{BC*BC) *AC ВС

00 01 II w

н=вс*ВО

Рис. 6.124. а) Пример цикла соглаоио диаграмме состояний рис. 6.122 и определение функции обратной связи F; б) пример другого цикла

Таким образом, очень просто получаем полную минимизацию алгебраического выражения функции F, логика которого может быть реализована на D-триггере с одним входом. А после несложного преобразования алгебраического выражения функции F опреде-

лим логические соотношения входов J и К. При использовании других типов триггеров процесс такой же. На рис. 6.1246 приведен пример решения другого возможного цикла.

На рис. 6.125 показаны примеры схем, которые могут быть использованы в качестве счетчиков или генераторов кодов с цик-

л лом согласно рис. 6.124. На рис. 6.125с схема на /)-триггерах, следующие схемы на (-триггерах демонстрируют решения на логических схемах И-НЕ, И/ИЛИ-НЕ и И-НЕ с объединенными выходами.

В приведенном примере функция обратной связи F сравни-; тельно проста, но она значительно усложняется с увеличением