ма. Другой способ автоматической установки требуемого цикла схемы показан на рис. 6.1286. Состояние ООО обнаруживается вспомогательной логической схемой на входе S первого триггера.. Если это состояние будет зарегистрировано, то следующим тактовым импульсом с выхода элемента И-НЕ с помощью асинхронного входа S в триггер А будет записана I, в результате чего схема установится в состояние 100 и требуемый цикл. Очень проста логическая схема при использовании (-триггеров - рис. 6.128е.

Составление схемы регистров с ОС с произвольным числом каскадов производится так же. В табл. 6.4 представлены функции обратной связи F для числа каскадов п=3-=-12 без автоматической установки цикла.

Таблица 6.5. Функции управляющих входов /, К, с учетом автоматической установки цикла

Функции управляющих входов J, К

Длина цикла 2"-1

Функции упраяляющих входов J. К

Длина цикла 2"-1

Обозначение каскадов - А В С В Е FGHIJKLMNOP.

У Номера каскадов -l 2 3 4 5 6 7 8 9 10 11 12 13 14 15,16.

. В табл. 6.5 представлены функции управляющих входов /, К с учетом автоматической установки цикла.

Сдвиговые регистры с обратными связями, имеющие длину цикла меньше 2"-1

При составлении схем можно воспользоваться несколькими методами. Если регистр имеет небольшое число каскадов п, то необходимую для данного цикла последовательность состояний можно выбрать, например, по общей диаграмме состояний. На рис. 6.129G цикл имеет длину L=6. Кроме требуемого цикла, возникают еще две петли (по одному состоянию), т. е. имеют место-заблокированные состояния 0-7. Решение с учетом автоматической установки нужного цикла представлено на рис. 6.;129б.

Следующий пример для случая Ь-Ъ показан на рис. 6.130. Из диаграммы состояний на рис. 6.130а видно, что, кроме желательного цикла под влиянием петли с состояниями 2 и 5, может возникнуть нежелательный цикл длиной L-2. Устранение этой нежелательной петли и автоматическая установка нужного цикла могут быть решены двумя способами - рис. 6.1306, в. Очевидно, что в-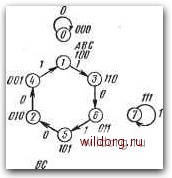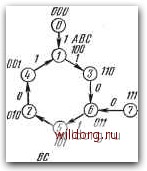

J=BC+BC

F~A С С UJ1U F=AC +АВ+АБС=АВСЩВ*(:)

А 00 01 И

Кл=В+С

S)

Рис. 6.129. а) Пример цикла длиной L-Ъ; б) решение с учетом автоматической установки нужного цикла

010 5)

АВС ООО

АВи ООО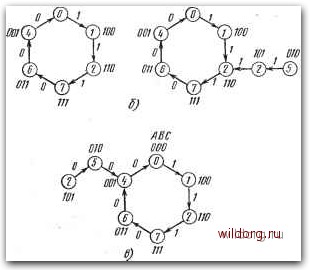

А 00 01 11 10

А 00 01 11 10

F=A{B*C)*AE J,=C

KfB*C=BC

F=AC-BC

Ja=bc

Рас. 6.130. a) Пример цикла длиной L=5; б), в) решение с учетом автоматической устаиовии нужного цикла

связи с возникновением нежелательных петель состояния 2 и 5 нельзя считать просто избыточными, которым в карте функций обратной связи F можно придать любые значения X, т. е. 1 или 0. Если, например, в поле ЛВС=101 карты на рис. 6.1306 записать значение Р=0, то получим очень простое алгебраическое выражение функции F = С, однако возникает петля состояний (рис. 6.130с). Так же, как в рассмотренных ранее случаях, возможны два способа решения:

а) переход из заблокированных состояний решают путем автоматической установки требуемого цикла, в результате получается сложная логическая схема входов первого каскада сдвигового регистра;

б) заблокированные состояния считают избыточными, и в карте соответствующей функции им придают любое значение, 1 или 0. При этом можно получить очень простую логическую схему. В данном случае необходимо исключить возможность возникновения нежелательных петель, используя принудительную установку регистра в нужное состояние с помощью подходящей комбинации сигналов на прямых, асинхронных входах триггеров.

На рис. 6.131 приведен пример решения сдвигового регистра с ОС, предназначенного для функции десятичного счетчика и составленного на основе диаграммы состояний на рис. 6.123.

Следующий метод, так называемый метод скачка, исходит из соответствующей функции обратной связи F в табл. 6.4, т. е. используются последовательности М. Пример решения для L=I0

DOOD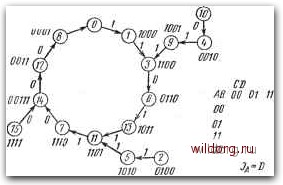

1<д=ВС*В1)

в -f

в в.

>

J А К А

J В К В

J ю -

Рис. 6.131. Пример синтеза сдвигового регистра с ОС, выполняющего функцию десятичного ететчика