
 |
|
Главная страница Систематические методы минимизации [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [ 57 ] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] ®®©(D®© ®(D®® ® ®® ®
SR 00 0.1 11 ID ® ID 10 10 01 01
01® 1)10
Puc. 6.19. Триггер типа E (ИСКЛЮЧАЮЩЕЕ ИЛИ): a) временная диаграмма; б) последовательность составления примитивной таблицы развития; в) результирующая примитивная таблица развития; г) дна-грамма объедннеиия; д) сокращенная таблица развитая Синтез -триггера с двумя петлями обратной связи показан на рис. 6.20. Принцип такой же, как у базового триггера типа ИЛИ-НЕ. На рис. 6.20а определяются алгебраические выражения функций Fl и Уг в виде, подходящем для реализации триггера на базе элементов ИЛИ-НЕ; алгебраические выражения функций Yi и Уг согласно рис. 6.206 целесообразно реализовать на элементах И-НЕ. Схемы обоих триггеров показаны на рис. 6.20в, г. Эти схемы идентичны, а сравнение карт переходов показывает, что идентичны и их свойства, т. е. очевидно, что их свойства одинаковы с точки зрения положительной и отрицательной логики. Это характерная особенность -триггера, отличающая его от других типов триггеров. Диаграмма состояний показана на рис. 6.21а. Представленные -триггеры, составленные на основе временной диаграммы, выполняют требуемую функцию только при соблюдении определенных ограничивающих условий, касающихся одновременного изменения сигналов на управляющих входах. Рассмотрим, например, устойчивое состояние 1 и одновременное изменение сигналов Я8 со значения 00 на 11. В зависимости от того, насколько отличаются величины внутренних дискретных задержек схемы, может иметь место переход или в устойчивое состояние 6 без изменения состояния Q1Q2 или в состояние 4 с изменением 176 У1Уг DO 01
Y2=yiS+yiB=yi(s+R}, Q2=yz 0) уу\ 00 0 /0 0? ID 00 01 11 10 00 01 11 10 00 01 11 10 ® © Yiyj+SR; Qf=yj y2=yi-tSR; 02=У2 ИЛИ-НЕ 01 ID J100 VOOOI r~d/~tT. "0001 1110 .0001 0101 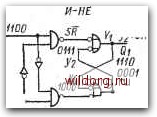 10 01 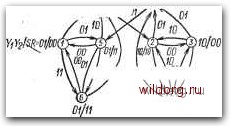 /11/10 or (D®(D(D(z)®® ® ®© SB Y2-yiSR ® fill Г"1 ® lif ® itiri ® ® ® ® ® ® UT" Puc. 6.20. Синтез -триггера с двумя петлями обратной связ-и: а) определение функций Fi и Уг в виде, пригодном для реализации на элементах ИЛИ-НЕ; б) для реализации на элементах И-НЕ; в) схема в базисе ИЛИ-НЕ; г) схема в Ptc. 6.21. а) Диаграмма состояний -триггера; б) временная базисе И-НЕ диаграмма состояний выходов QiQz- Заранее нельзя определить результирующее состояние. Аналогично при изменении сигналов iRS со значения 11 на 00 может произойти переход из устойчивого состояния 6 в состояние 1 или 3. Поэтому для обеспечения правильной работы схемы нужно добиться последовательного изменения сигналов на входах R и S. Одновременные изменения со значения 01 на 10 и наоборот допустимы, так как результирующие последовательности стремятся всегда только к одному устойчивому состоянию. Работу схемы на практике демонстрирует временная диаграмма на рис. 6.216. Для обеспечения рабочих условий, соответствующих заданной временной диаграмме, состояние покоя .входов обеих схем должно быть JRS=00. Однако анализ этих схем показывает, что они могут ®®®(D®©®®®® ® © @
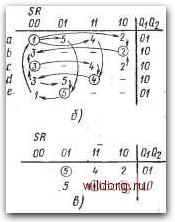 tf,e ® - 6,c,d® 00 Oi 11 10 DO 01 11 10 DO 01 11 10- 00 01 11 10  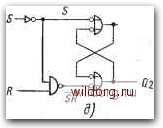 yry2+SiY2=yi-SR - Yry2S;Y2yiS+yiR YryiS Yry2+S V-*-Di Yi=y+SR 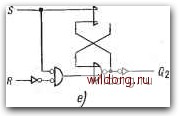 Y2=y+SR Puc. 6.22. Синтез S-триггера: a) временная диаграмма; б) составление примитивной таблицы развития; е) сокращенная таблица развития; г) карты; д, е) результирующие схемы на элементах И-НЕ и ИЛИ-НЕ [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [ 57 ] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] 0.0092 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||