6 5 АСИНХРОННЫЕ СЧЕТЧИКИ НА СИНХРОННЫХ ТРИГГЕРАХ

Самые простые схемы счетчиков с минимальным количеством логических схем возникают при использовании обратных связей с выходов собственных триггеров. У синхронных счетчиков тактовые импульсы подаются параллельно всем триггерам счетчика, которые одновременно реагируют на активный фронт тактового импульса. У счетчика с собственным управлением тактовые импульсы подаются только на вход первого триггера, а входы следующих триггеров управляются выходами предыдущих триггеров, т. е. в принципе эти счетчики работают асинхронно.

На рис. 6.99G, б показаны схемы счетчиков, работающих в направлении сложения и вычитания, которые могут зарегистрировать всего 16 состояний. При анализе и синтезе данных счетчиков необходимо заранее знать, на какие изменения тактовых импульсов

Рис. 6.99. а) Асинхронный суммирующий счетчик с 16 состояниями; б) вычитающий; в) временная диаграмма счетчика «а»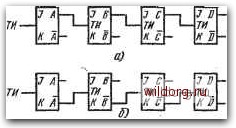

; 2 3 и 5 .6 7 8 9 т 11 12 13 Ik К Ю

jiruiJimiriJiJinminji -j~i rn j~-r~L

I * i L I--L

реагируют используемые триггеры. Допустим, что имеется схема на рис. 6.99G и что состояние триггера изменяется при изменении тактового импульса со значения ТИ=1 на ТИ=0. При переключении первого триггера с Л = 0 на Л=1 состояние триггера В не меняется. Под действием второго тактового импульса значение Л = 1 изменится на Л = 0, а это уже оказывает воздействие иа триггер В, т. е. триггер В переключается после каждого второго импульса. Отсюда следует, что триггер С меняет свое состояние после каждого четвертого импульса, а триггер D - после каждого восьмого импульса, как это показано на рис. 6.99.

Таким образом, если должен переключиться определенный триггер счетчика, то все предыдущие триггеры должны изменить

9-2.Я 257

свое состояние со значения 1 на 0. Это аналогично прибавлению двоичной 1 к двоичному числу, содержащему только единицы. Если прибавить 1 к цифре младщего разряда, то получается О и перенос 1 в более высокий разряд и т. д. Допустим, что состояние счетчика ABCD=lllO. Под действием тактового импульса на входе триггера А он переключится из состояния 1 в состояние 0. Это изменение воздействует на триггер В, который изменит свое состояние с В==1 на В = 0. А это изменение, в свою очередь, воздействует на триггер С и т. д. до тех пор, пока результирующее состояние счетчика не будет ABCD = 000l. Задержки, имеющие место при переключениях в отдельных каскадах, складываются, и при определенной величине общей задержки по отнощению к частоте входных импульсов счетчик перестает правильно работать. Влияние этой задержки должно быть, конечно, учтено и в случае дешифрирования выходов, однако у счетчиков данного типа дешифратор обычно не используется. Задержка не вызовет помех, если счетчик используется только для деления входных частот, так как в данном случае нас интересует только частота на выходе последнего каскада счетчика. По сравнению с синхронными счетчиками быстродействие асинхронных счетчиков с последовательным переносом значительно меньше. Однако у данных счетчиков быстродействие не является главным требованием, они применяются прежде всего из-за своей простоты.

Анализ и синтез этих счетчиков не так прост, как синхронных, поскольку нужно заранее определить, какие выходы триггеров будут использованы для управления входами следующих триггеров.

Рассмотрим, например, синтез десятичного счетчика в коде 8421 (таблица на рис. 6.100). Предположим, что использованы (-триггеры, реагирующие на изменение тактовых импульсов со

Рис. 6.100. Пример синтеза десятичного асинхронного счетчика

значения ТИ = 1 на ТИ = 0. Ясно, что состояние выхода А изменяется после каждого тактового импульса. Далее очевидно, что состояние выхода В изменяется после каждого изменения выхода А со значения 1 на 0. Изменения с Л = 0 на Л = 1 на состояние выхода

в не влияют, поэтому выход А может быть использован для управления триггером В, т. е. ТИв=А. Для управления триггером С можно использовать выход А или выход В, так как выход С изменяет свое состояние при изменении с В=1 на В=0 и при изменении с Л = 1 на А = 0. Использование выхода В, т. е. ТИс=В, приводит к более простому решению, что связано, как это будет показано далее, с наличием большого числа избыточных состояний. Для управления входом D может быть использован только выход А, потому что состояния выходов В и С не меняются при переходе из состояния 9 в состояние 0.

Таблицы входов /, К составляются по следующим правилам:

1. Если состояние управляющего выхода не меняется или меняется со значения О на 1, то состояние соответствующих входов обозначается символом X. Этот символ в принципе означает, что подготовительные сигналы на входах /, К, необходимые для синхронного режима работы, в рассматриваемом случае излишни. Значит, символы X отмечают неопределенные состояния, позволяющие упростить логическую схему.

2. Для остальных изменений управляющих входов справедлива программная таблица, рассматриваемого типа триггера.

Рассмотрим, например, входы /, К триггера С, управляемого выходом В. После перехода из состояния О в состояние 1 выход В не изменяется, поэтому в строку, соответствующую состоянию О,, запишем JcKc=XX. При переходе из состояния 1 в состояние 2 значение выхода В изменяется с О на 1, однако это изменение-не влияет на триггер С, поэтому в строку, соответствующую состоянию 1, запишем значения JcKc=XX. После перехода из состояния 2 в состояние 3 выход В не меняется, поэтому состояниюг 2 соответствуют опять значения JcKc~XX. При переходе из состояния 3 в состояние 4 выход В переключается со значения 1 на О, а это изменение должно повлиять на выход С, который из состояния О переходит в состояние 1. Согласно программной таблице (-триггера должно быть /с=1 и Кс = 0- Таким же образом определяются значения входов всех триггеров для всех состояний, счетчика.

Данные из таблицы на рис. 6.100 записываем в карты на; рис. 6.101а и определяем алгебраические соотношения, выражающие функции входов /, К отдельных триггеров. Простота логической схемы вытекает из большого числа неопределенных состояний. Так как это десятичный счетчик, то шесть неопределенных состояний можно получить, исключив состояния 10-15 двоичного кода 8421, а другие неопределенные состояния вытекают из синтеза рабочих условий в таблице на рис. 6.100. Результирующая схема показана на рис. 6.1016. Сначала начертим соединения, соответствующие выходам, которые непосредственно управляют вхо- дами следующих триггеров. В рассматриваемом примере - эта соединения выхода А с входами ТИ триггеров В и D ч соединение выхода В со входом ТИ триггера С. Теперь остается нарисовать 9* 2591