Результирующая функция имеет вид

+ {А,В,+А,В) {АВ,) {Ai+B)+(AB+A,) {А,В+А,В) Q.

Пример реализации показан на рис. 5.43а. Структурная схема п-разрядного сумматора представлена на ряс. 5.43е. Кроме пред-

ABi, Aj Вз

A2B2

А, В;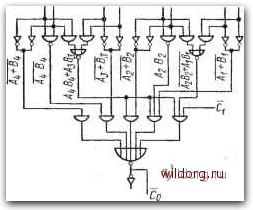

Bt, Bj В2 Bj Ац As А2 Af

Bp Bn-lBn-2Bn-3

An V/-"/? 2-,7-3

Be By Be Bs BiBjBzBf 8 h % h 1, h Az A,

Ускоренный C/T-cj перенос

По модулю

Sii S3 S2 Sj

Sy 5g Ss Sii Sj 62 5/

Puc. 5.43.a) Схема ускорения переноса; б) символ четырехразрядного сумматора.с ускорением переноса; е) п-разрядный сумматор

ставленного метода, существуют еще и другие варианты решения сумматоров с ускоренным переносом, которые в данной книге не рассматриваются.

Сложение и вычитание двоичных кодов десятичных цифр

В комбинационной таблице на рис. 5.446 комбинации StSgSzSi представляют собой результирующую сумму, полученную четырехразрядным двоичным сумматором, а С4 - перенос в старший разряд. Комбинации S4kS3k52kSik представляют требуемую сумму двоичных кодов десятичных цифр, а Сак - требуемый перенос в старший разряд. Из таблицы видно, что суммы правильны только

Si2 Cm=0 CuK=f

S1S2 CiK=0 S2K Ct,k=1

C,,H-S2Si,*SiS-C„ S2K?Ci,k+S2C,,k; S2K=S2 Ci,KiSz CuK

S3Kj3Ct,K+S2S3CM + S2SjCKi S3K = S3CuK-S2S3Cw+S2S3Cw \K -SuCuK + S2CuKi SuK=S<, с ЦК +5ц Сцк +5ц Сц + 5 Сцк

Рис, 5.44. Составление схемы сумматора двоичных кодов десятичных цифр: а) комбинационная таблица; 6) минимизация выходных функций

ДО цифры 9. При сложении двоичных цифр возникает перенос Ci=l, если результирующая сумма 516; при сложении двоичных кодов десятичных цифр должен быть CiK~\, если результирующая сумма 5к10.

Алгебраическое выражение возникновения переноса можно получить прямо из .комбинационной таблицы выходов Si-S4 и С4. Корректирующие цепи, предназначенные для исправления результирующей суммы, можно составить на основе алгебраических выражений функций 52к, 5зк и 54к, полученных из карт на рис. 5.446. Из комбинационной таблицы вытекает, что Sik=5i. На рис. 5.45а - пример схемы, реализованной в базисе И-НЕ, На рис. 5.546 для коррекции суммы использован элемент ИСКЛЮЧАЮЩЕЕ ИЛИ, неполный и полный сумматоры. Принцип действия корректирующих цепей очень прост. Если сумма равна или больше 10, то корректирующая цепь прибавляет цифру (6)10=1(0110)2, причем возникающий перенос не учитывается.

Корректирующие цепи могут бьггь составлены так, чтобы на их выходах результат сложения был в любом требуемом коде. На

<=оршро- \з Вг л, ; eoHueCifKi J-1-и-U-Li

I I---Ц четырарпзрядиий суннтр

АВ AiBi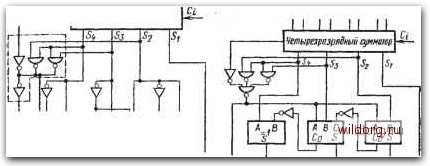

P«c. 5.45. Примеры схем, производящих сложение двоичных кодов десятичных цифр:

в) схема коррекции в базисе И-НЕ; б) для коррекции использованы элементы И-НЕ, ИЛИ-НЕ, узел равнозначности, неполный н полный сумматоры

Рис. 5.46. Примеры схем суммирования Двоичных кодов десятичных цифр с выходом в коде с избытком 3: о) комбинационная таблица; б) схемы с элементами И-НЕ и ИСКЛЮЧАЮЩЕЕ ИЛИ; в) схема с двумя четырехразрядными сумматорами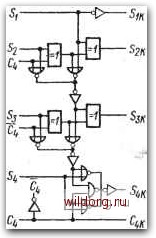

Ai,Bif AjBj а2в2 AiBj

Четюехтрядиай lymamii

Su S3 Sz Si

CflJ Четырехразрядный сумматор