
 |
|
Главная страница Систематические методы минимизации [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [ 34 ] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] же вносятся в карту как символы X. После определения мини- мизированных алгебраических выражений функций В2С2 преобразование можно осуществить с помощью двух схем И-НЕ. Последовательность синтеза обратного преобразователя (см. рис. 5.8) аналогична. На рис. 5.9 представлен процесс составления схемы преобразователя кода 8421 в код с избытком 3. Используя карты на рис. 5.96 производят минимизацию выходной функции преобра-
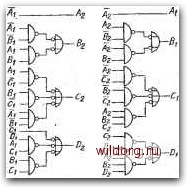 СгА,С+В,С/А,В,С, А,=Аг BfABfABi B-AiBL/CVz Рис. 5.9. Процесс -составления схемы взаимного преобразования кодов 8421 .и с избытком 3: а) комбинационная таблица; б) минимизация выходных функций для преобразования кода 8421 в код с избытком 3; в) результирующая схема в базисе И-НЕ; г), д) минимизация выходных функций и результирующая схема преобразования кода с избытком 3 в код 8421 зователя кода 8421 в код с избытком 3 (результирующая схема На базе И-НЕ - на рис. 5.9в). Последовательность синтеза обратного преобразователя показывают карты на рис. -5.92, схема представлена на рис. Ъ.9д. Из карт наглядно видно, что неиспользованные комбинации X позволяют значительно упростить выходные функции. Для полноты представлены и карты выходных функций Лг, Ль В этих картах нет необходимости, так как срав- нением соответствующих столбцов комбинационной таблицы получаем, что А2=А\ и А\=А2. На рис. 5.10- представлен процесс составления схемы преобразования кода 8421 в код Грея. Из карт на рис. 5.106 вытекает.
=/ -с. -"1 с,р\оо 01 и 10 Об р( и }й Ш Pf If 10 СЖООа 11 10 op Of 1110 во PI 1? Id
АггЩЩВ1 Bz-efitPjC, Сг=Щ*В, Puc. 5.10. Процесс составления схемы взаимного преобразования кода 8421 и кода Грея: а) комбинационная таблица; б) минимизация выходных функций преобразования кода 8421 в код Грея; е) результирующая схема на узлах равнозначности; г), д) минимизация выходных функций и результирующая схема преобразования кода Грея в код 8421 что этот перевод может быть реализован с помощью трех узлов равнозначности (рис. 5.10в). Из комбинационной таблицы видно, что Di = D2. Обратное преобразование более сложно. Выходная функция имеет вид • + ЛДед+ЛВДОа+ЛгВгед-Функцию Bi можно преобразовать следующим образом: • Точно так же преобразуем функцию Aii Результирующая схема с тремя узлами равнозначности представлена на рис. 5Л0д. Схема, естественно, можеТ быть составлена из комбинации любых подходящих элементов. На рис. 5.11 приведен при- 4? ---ту мер построения схемы в базисе И-ИЛИ-НЕ и И-НЕ. Преобразование двоичного кода де- -2 сятичных цифр более сложно. Из ком- бинационной таблицы на рис. 5.12 вид- Сг но, что двоичный код десятичной ЦИф- gg-jN ры 9 (в коде Грея) отличается от со- -U L-tv ответствующего значения в комбина- ZZf)- ционйой таблице на рис. 5.10а. После-довательность составления схемы на рис. 5.12в такая же, как и раньще. На рис. 5.13 показано составление схемы преобразования двоичного кода десятичных цифр в код, соответствующий семиэлементному отображению 4-десятичных цифр О-9. Десятичные цифры, выр-аженные с помощью ком-бинаций сегментов, можно видеть на gjj схема преобра- рис. 5.13а. По комбинационным табли- зования кода Грея в код цам на рис. 5.13в составляются карты .8421 в базисе И-НЕ, минимизации выходных функций, со- И/ИЛИ-НЕ ответствующих отдельным сегментам a-g. Пример схемы в базисе И-НЕ представлен на рис. 5.14. На дешифрованном выходе - уровень В, что является выгодным, так как к выходам а-g можно подключить простые мощные транзисторные инверторы, управляющие соответствующими сегментами. Пунктирной линией показано необходимое число корпусов типовых интегральных схем. Выявление неиспользованных комбинаций в коде. Определение неиспользованных комбинаций позволяет сравнительно просто обнаруживать ошибки в некоторых кодах. Рассмотрим, например, двоичный код 8421 десятичных цифр. Из таблицы на рис. 5.15 вытекает, что из общего числа шестнадцати возможных комбинаций четырех переменных шесть комбинаций - избыточные. Расчет детектора этих неиспользованных комбинаций прост. Каждой неиспользованной комбинации будет со- 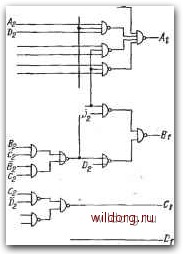 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [ 34 ] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] 0.0089 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||