При использовании интегральных схем каждая схема на рис. 5.17в, г представляет собой один элемент (корпус).

Сложность составления схемы сравнения для обнаружения неравенства (неравнозначности) возрастает с р.остом числа бит сравниваемых информационных данных Л и В. На рис. 5.18а представлен пример простого одноразрядного узла сравнения. Алгебраические выражения функций F2 и можно определить прямо из комбинационной таблицы. Составление схемы узла сравнения двух бит на рис. 5.186 значительно более сложно. В качестве примера приведена реализация функции F2 и Рг на элементах И-НЕ с двумя входами. На рис. 5.19а показана реализация тех же функций на базе элементов И-НЕ с двумя и тремя

A,A2

BjBKgoonfjo oo\ 1 \[о \шш

шишш

MML.

Fi=UjB,+AiBi){AzBz+AzBz)

a) -

AiBi+AiBi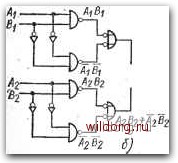

g=t>i

-(A,B,+AiBi){A2Bz+A2B2)

Рис. 5.17. Последовательность составления цепи определения равнозначности двух переменных-А и В:

а) комбинационная таблица и минимизация выходной функции; б), в), г) результирующая схема

Ff-AB + AB Fz=AB; FsAB

§2

fBiA2B2

AiA2

oo\ oMMi\\o\o\o\o\ 10[£1т\о\Цр\о[Щ

F2 F3 Fz =A2Bz +AiAzBi-t-Ai BfBz Fj=A2B2-AlA28fi-A,BB2

AB \

Ф-~А<В

ZIFj=fl2Bz+AiBi.AzBz AiBtA2B2 AB

AjlM

Рис. 5.19. а) Цепь сравнения двух б) цепь сравнения четырех бит

бит:

Рис. 5.18. а) Цепь сравнения одного бита; б) щель сравнения двух бит

входами, на рис. 5.196 - схема узла сравнения четырех бит. Обратим .внимание на структуру обеих схем, которая позволяет достаточно просто составлять узлы сравнения большого числа бит. У всех представленных схем активный выход соответствует уровню В..

5.5. ДОПОЛНЕНИЯ

Формирование дополнений двоичных чисел требуется, как было показано раньше, прежде всего при выполнении арифметической операции вычитания. Вместо прямого вычитания данного двоичного числа определяется его дополнение, которое прибавляется. Эти схемы составляются так, чтобы они позволяли не только получать дополнение данного числа, но и передавать данное число без изменения. Использование такой схемы обеспечивает простую реализацию сложения и вычитания данных чисел. Самым простым является получение дополнений до 1, прин-• цип которого заключается в инверсии всех входных переменных, как показано на рис. 5.20а. В этой простой схеме на выходах ин-

Рис. 5.20. а) Простая схема получения дополнения до 1; б), в) схемы, обеспечивающие передачу на выход информации в нрямом коде либо в дополнениях до единицы

С -4

1-е,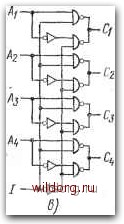

верторов получается дополняющее число С, как только на входах имеется данное число А. На рис. 5.206 представлена схема, обеспечивающая прямую передачу входного числа А на выходы. В качестве базовой может быть использована схема ИСКЛЮЧАЮЩЕЕ ИЛИ. Рассмотрим, например, схему, имеющую выходную функцию Ci=-AiI-{-Ad. Если /=0, то Ci=Au что означает передачу входной переменной на выход Ci без изменения. Если /= = 1, то Ci=A, что означает получение на выходе Ci инверсии входной переменной А. Отсюда вытекает принцип действия схемы на рис. 5.206. Если /=0, то на выходах будет входное двоичное число без изменений, если /=1, то на выходах создается дополнение до единицы С числа Л. Другими словами, /=1 означает инверсию. Другой пример схемы на базе И-НЕ показан на рис. 5.20в. Пред-