ставленные схемы можно рекомендовать для кода 2421 и кода с избытком 3.

В натуральной двоичной системе используются двоичные дополнения, представляющие собой дополнения до 1, к младшему разряду которых прибавляется двоичная 1. Пример расчета приведен на рис. 5.21. Из комбинационной таблицы вытекает, что Ci = =Ai. Из карт получаем минимизированные функции Сг, Сз и С4, которые преобразуем таким образом, чтобы схема позволяла не только получать двоичное дополнение С входного числа А, но и передавать число А без изменения. Преобразование просто:

Q= (ЛзЛ,+ли4+44+Л4зА+Л

Пример реализации схемы в базисе И-НЕ представлен рис. 5.21.

.двоичные

Cf

Cl-AiAi+iAi

Ci=AKsl2ifihl

С=/1з A+A{A,*A2Ai+A)A2Ajif CyAjA2+JiT2

=/lj/Ij+>42/lj+-4,/l2J

Cit=A3AiA.lA+A2Ai,AfA2A;Tii.

Puc. 5.21. Составление схемы, обеспечивающей получение двоичных дополнений: а), б) комбинационная таблица и минимизация выходных функций; е) результирующая схема в базисе И-НЕ

На- рис. 5.22 показан пример составления схемы создания дополнений двоичных кодов десятичных цифр. Из комбинационной таблицы видно, что Ci=Ai и С2=А2. Упрощение алгебраического

-Дополнение

Неиспользованные комбинации

а\00 Of 11 10 00 01 11 10

Cz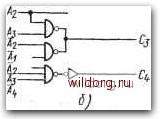

Аг-Аз-

cO-c«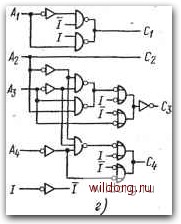

Puc. 5.22. Составление схемы получения дополнений двоичных кодов десятичных цифр:

а) комбинационная таблица; б) минимизация выходных функции и результирующая схема; б), г) схема получения дополнения нли передачи информации без изменения

выражения функции Сз позволяет произвести неиспользованные комбинации, обозначенные в картах символом X. Для сравнения на рис. 5.226 имеется простая схема, создающая только дополне-

ние, а на рис. 5.22г - примеры схем, обеспечивающих или получение дополнений, или.передачу числа А без изменения в зависимости от состояния входа /.

5.6. КОНТРОЛЬ ЧЕТНОСТИ

Принцип контроля четности был объяснен в § 3.3. Он очень важен потому, что позволяет производить сравнительно простой контроль операций, осуществляемых в системе при обработке цифровой информации. Для практического применения необходимы, во-первых, цепи, создающие бит четности, так называемые генераторы четности, а во-вторых, цепи контроля четности. Каждая цепь может быть составлена так, что контролируется четность или нечетность. В первом случае на выходе цепи 1 будет только тогда, когда 1 имеется на четном числе входов, а во втором случае, наоборот, 1 на выходе будет только тогда, когда 1 имеется на нечетном числе входов. Самой простой схемой с контролем нечетности является ИСКЛЮЧАЮЩЕЕ ИЛИ с двумя входами, которую очень просто можно преобразовать для контроля четности. Основные схемы были представлены в табл. 5.1, они позволяют сравнительно простое составление многих схем с контролем четности.

На рис. 5.23 показано составление схемы контроля нечетности комбинации четырех бит: Л4Л3Л2Л1. Из комбинационной таблицы видно, что Р=\ только при нал1ичии нечетного числа единиц в соответствующей комбинации. Из карты функции Р вытекает, что результирующее алгебраическое выражение функции Р нельзя минимизировать. Основное алгебраическое выражение в форме дизъюнкции конъюнкций имеет поэтому вид

р=лДЛз4+лИ244+А444+44Л+

+AiAAgA-j- AiAAgA- АААА+ЛЛдЛзЛ. Его можно преобразовать:

Р={АА+АА {АА+А,А,)+{А,А,+АА,) (ЛзЛ,+ЛзЛ=

ел,) (4ё4)+(4ёЛ) (ЛзфЛ,).

На рис. 5.236 показан пример реализации схемы на трех элементах равнозначности, составленных из базовых функциональных схем типа И-НЕ. Контроль показывает, что требуемая четность Р имеет место на выходе Pi. Если 1 (уровень В) имеется на нечетном числе входов, то Р = 1 (уровень В) на выходе Pi. Для контроля нечетности в выходе Рг нет необходимости, он изображен для полноты функциональных возможностей схемы. Действительно, если правильная четность на выходе контрольной схемы или четность на выходе генератора четности представляются значением 1, то выходы Pi и Рг на рис. 5.236 будут иметь следующее назначение: 118