
 |
|
Главная страница Систематические методы минимизации [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [ 28 ] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128]
Другими словами, на входе - положительная логика, а на выходе - отрицательная логика. Для использования символов теперь важно понятие совпадения и несовпадения логических полярностей,. которое подробно объяснено на рио. 4.8. Считаем,, что на входах схемы на рис. 4.8а положительная полярность- В, она изображена в скобках. Так как на входах символа функции И нет кружков, то положительная полярность Х(Ъ), У(Ъ) совпадает с положительной поля1ностью входов символа. Совпадают также отринательные полярности, обозначенные кружками на выходе символа функции И и на входе символа инвертора. Так как рассматриваем положительную полярность выходной функции F, а на выходе сим- вола инвертора тоже положительная полярность, то логические лолярности совпадают и на выходе. Логические прлярнаети входных переменных X. Y и выходной функции F совладают, поэтому можно прямо написать, что F=XY. y(Bj- J( YlBj У{В) F=X76) F=WB) Рис. 4.8. Принцип совпадающих и несовпадающих логических полярностей: а) совпадение полярностей на входах и выходах; б) несовпадение полярностей на выходе; е) несовпадение полярностей на выходе; г) несовпадение полярностей на одном входе Обратим внимание на значение символа инвертора. Использование этого символа с кружком на входе исключает несоответствие логической полярности между и выходом (Щ символа функции И. Если же рассматривать значение символа с логической точки зрения, то придем к заключению, что этот символ не имеет никакого влияния на логическое значение, так как на его входе - отрицательная полярность с логическим значением 1, а на выходе - положительная полярность, которая также имеет логическое значение 1. Значит, символ представляет логическую тождественность и при чтении схемы не учитывается. На рис. 4.86 логические полярности на входах совпадают, а на выходе нет. На выходе символа слева от вертикальной пунктирной линии - отрицательная полярность (Щ с логическим значением 1, а справа от прямой (Щ имеет логическое значение О, так как здесь рассматривается положительная полярность (Ъ) с логическим значением 1. Это несовпадение логических полярностей на выходе означает изменение логического значения, причем физический уровень сигнала не меняется. Поэтому F=XY. На рис. 4.8в рассматриваются входные переменные Х(). У(Щ с отрицательной полярностью. Несовпадение логических полярностей Х(Щ, У(Щ и. соответствующих входов символа функции И исключается за счет использования символов инверторов с кружками на входах. Однако на выходе символа функции А имеет место несовпадение логических полярностей, поэтому F- =ХУ. На рис. 4.8г представлен символ логического сложения ИЛИ№ 8. Из табл. 4.5 отрицательная полярность Х(Щ совпадает с отрицательной полярностью, обозначенной кружком на входе символа, на другом входе У (В) имеет место несовпадение логических полярностей, а на выходе логические полярности совпадают, поэтому F=X+Y. Представленные примеры позволяют сформулировать основные принципы применения двойственных символов: а) двойственные символы логического сложения и умножения) определяются по табл. 4.5 в соответствии с таблицей уровней, функции используемой цифровой схемы; б) отрицание переменных имеет место всегда в случае несовпадения логических полярностей на входах, на выходе и между символами; в) с точки зрения логики символ инвертора с одним входом: представляет логическую тождественность. Он используется для исключения несовпадения логических полярностей, если не требуется отрицание соответствующей переменной, или, наоборот,, для получения несовпадения полярностей, если требуется отрицание переменной. Преимуществом использования двойственных символов является очень простое и наглядное изображение логических функций без трансформации их алгебраических выражений, которые, в-принципе, изображены графически. Также просто определяется" алгебраическое выражение логической функции данной логической схемы. Во всех последующих объяснениях предполагается использование цифровых схем с уровнем В, соответствующим определенному положительному напряжению, и с уровнем Н, соответствующим примерно нулевому напряжению, причем уровень В соответствует логической единице, уровень Н - логическому нулю. 4.6. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ И СЛОЖЕНИЕ НА ОБЪЕДИНЕННЫХ ВЫХОДАХ У некоторых основных схем можно получить дополнительную» логическую функцию прямым соединением их выходов. Типичные примеры таких схем имеются на рис. 4.9. Рассмотрим сначала Рис. 4.9. а) Две схемы ДТЛ с объединенными выходами; б) изображение логического сложения; е) изображение логического умножения; г) использование логики на объединенных выходах соЛшТ уменьшает необхо- димое схем количество 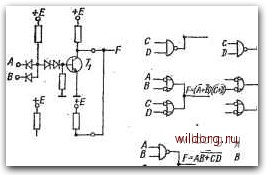 F=AB*CW [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [ 28 ] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] 0.0095 |