На рис. 6.109а представлена временная диалрамма счетчика, на выходе Z которого появляется импульс после каждого седьмо- / го входного импульса X. Диаграмма состояний не показана, так как она очень проста, причем ей соответствует последовательность состояний на временной диаграмме. Таблица состояний показана на рис. 6.1096. Выход Z зависит только от внутреннего состояния счетчика, т. е. это модель Мура последовательностной схемы. Счетчик имеет семь состояний, поэтому, он должен содержать три триггера, обеспечивающих 2=8 состояний. Таким образом получается одно избыточное состояние, позволяющее упростить комбинационпую логику. Главной проблемой является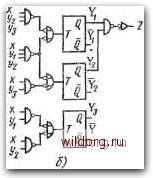

Puc. 6.110. Схема счетчика рис. 6.109: a) счетчик на С-тригге-рах; б) на Г-триггерах

выбор подходящего кода для трех внутренних переменных, так как от него зависит сложность комбинационной логики счетчика. Для восьми внутренних состояний существует 8!=4-10 возмож- ных вариантов. Выбранный код представлен в таблице на рис. 6.1096. Теперь таким же образом, как у синхронных схем, составляются программные карты входов, соответствующих данному типу триггера. На рис. 6.109в приведены программные кар-, ты / К-триггеров, а на рис. 6.109г - программные карты Г-триг-геров. Карта выхода Z имеется на рис. 6.109. Соответствующие схемы на (-триггерах и Г-триггерах показаны на рис. 6.110.

JlJTJUUlJUlJl rW

-L r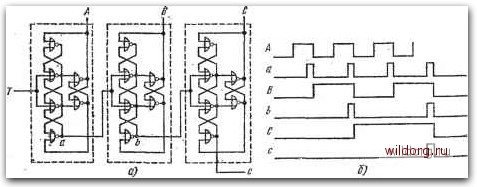

Рис. 6.111. а) Асинхронный импульсный счетчик на асинхронных симметричных Г-триггерах; б) временная диаграмма счетчика

Ylpn выборе другого кода внутренних переменных схема может получиться более сложной или более простой. Представленные счетчики с импульсным выходом иногда называют импульсными счетчиками.

Рис. 6.112. а) Асинхронный десятичный импульсный счетчик на асинхронных симметричных Г-триггерах; б) временная диаграмма счетчика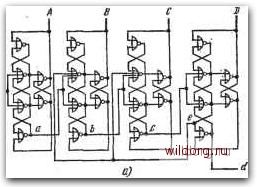

rJUUIJlJLJLJUUlJLJW n J-n J-L-ri r

Л П П П П

в \-1 г

с

-Ц-L

Л fl

"11-1

Г~~Т

Асинхронные импульсные триггеры во многих случаях позволяют создать схемы счетчиков сравнительно несложным путем. На рис. 6.П1а показана схема на асинхронных симметричных Т-триггерах. На выходе с появляется импульс при каждом восьмом входном импульсе. Обратим внимание, что для управления входами следующих триггеров использованы не выходы А, В, С, г вспомогательные выходы а, Ь, с. Принцип действия вытекает из временной диаграммы на рис. 6.1116.

Схема и временная диаграмма десятичного счетчика на тех же Г-триггерах представлены на рис. 6.112. Для ограничения числа состояний до десяти использована обратная связь с выхода четвертого триггера. В реверсивном счетчике на рис. 6.113 использованы ассиметричные Г-триггеры. Емкость счетчика состав-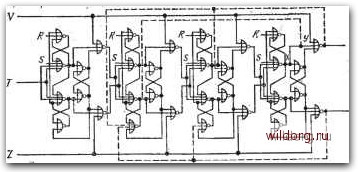

Рис. 6.113. Реверсивный асинхронный счетчик с коэффициентом пересчета 16

ляет 16 импульсов. Десятичный реверсивный счетчик получим введением связей, обозначенных пунктиром, и разрывом связи между выходом х и входом у.

6.7. КОНТРОЛЬ РАБОТЫ СЧЕТЧИКА

Для контроля правильности работы счетчика могут быть использованы методы, рассмотренные ранее в главах с комбинационными логическими схемами. Сравнительно просты, но дороги методы полного или частичного дублирования. У счетчиков с неполным использованием всех состояний правильную работу до некоторой степени можно контролировать с помощью детектора не-

Cff\ 00 or 11 to

Изменение четнота=-A*BC

Триггер i четности I

6) .

Puc. 6.114. Контроль счетчика с помощью четности:

с) таблица состояний двоичного счетчика с il,6 состояниями; б) минимизация алгебраического выражения изменения четности; в) контрольная цепь