входные переменные имеют значение 1 или О, т. е. она определяет равнозначность переменных А к В.

Примеры логических схем представлены в табл. 5.1. Эти схемы являются базовыми при проектировании самых разнообразных схем, примеры которых будут приведены далее. Для упрощения начертания логических схем удобен неориентированный символ. -На рис. 5.1 представлены ос-

новные символы без индикаторов состояния входов и выходов и символы с индикаторами состояния входов и выходов соответствующими таблицами уровней В и Н. Каждому реальному включению схе- мы соответствует только од- ц в на из представленных таблиц в н уровней. Интерпретация сим- * ® волов очень проста:

символ а: выход F в сое-

Всповиыеси,, состояния Вхоаав

в-\.

=1 -F

ОсноВныбсимВолы с индикаторами состояния ВхоШ н Выходов

-F=A@B

-F=AeB

-F=A@B

тоянии в только тогда, когда любой из входов находится в в н состоянии в, а другой - в со- в в стоянии Н;

символ б: выход F в состоянии В только тогда, когда

любой из входов находится в С«1°" предназначенные для

U . логической функции равнозначности и

состоянии п, а второй в со- неравнозначности двух переменных - А стоянии В; и В

символ в: выход F будет в состоянии Н только тогда, когда вход А находится в состоянии Н и вход В - в состоянии Н или когда вход В и вход А находятся в состоянии В;

символ г: выход F находится в состоянии Н только тогда, когда вход В находится в состоянии Н и вход А - в состоянии Н или если вход А находится в состоянии В и вход В - в состоя- . НИИ В.

Все четыре символа отвечают соответствующей таблице уровней. Аналогично интерпретируются значения символов д-З, соответствующих другой таблице уровней.

5.3. ШИФРАЦИЯ, ДЕШИФРАЦИЯ И ПРЕОБРАЗОВАНИЕ КОДОВ

Схемы, предназначенные для преобразования цифровой информации из десятичной системы счисления в двоичную, обычно называются шифрирующими, а для обратного преобразования - дешифрирующими. Схемы, предназначенные для преобразования .различных кодов в двоичной системе, называют преобразователями кода.

Шифраторы. Составление таких схем очень простое. На рис 5.2 представлен пример расчета схемы преобразования де-

код 8 4 2 1

код 1 из 10

(У -

ИЛИ-НЕ

3-Б-7-

% В 7

И-НЕ

Рис. 5.2. Составление схемы преобразования десятичных цифр О-9 в код 8421:

а) комбинационная таблица; б) результирующая схема на базе элементов ИЛИ-НЕ; е) на базе элементов И-НЕ

сятичных цифр О-9 в код 8421. Из комбинационной таблицы на рис. 5.2а видно, что двоичным цифрам 1 в столбике А соответствуют десятичные цифры 1, 3, 5, 7 и 9, т. е. можно написать: Л = = 1 + 3+5-Ь7+9. Это - алгебраическое выражение логического сложения. Точно так же справедливо, что

5=2+3+6+7, С=4+5+6+7, £)=8+9.

На рис. 5.2 представлен пример реализации схемы на элементах ИЛИ-НЕ. В состоянии покоя на всех входах - уровень Н. В схеме на рис. 5.2в у элементов И-НЕ в состоянии покоя на всех входах - уровень В. Подобным образом можно составить схемы преобразования десятичных цифр в любой код. Примеры некоторых схем имеются на рис. 5.3.

Дешифраторы. Проектирование схем дешифраторов также простое. На рис. 5.4 показан процесс составления схемы, предназначенной для преобразования кода 8421 в десятичные цифры. В комбинационной таблице, представленной на рис. 5.2а, имеется шесть избыточных комбинаций кода 8421. На рис. 5.4а эти неиспользованные комбинации обозначены в отдельных картах символом X, они могут иметь любое значение, 1 или О, и поэтому позволяют упростить результирующие алгебраические выражения. В качестве примера представлены карты цифр 4 и 8. Для расчета, однако, достаточно одной карты, из которой можно получить все минимизироваиные выходные функции, соот-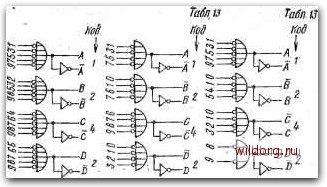

И-НЕ

И-НЕ

И-НЕ

И-НЕ тЗплкстри И-НЕ кодМжоисвна

Рис. 5.3. Примеры схем преобразования десятичных цифр в различные коды

J>-

B=/\D

Cd\DD 01 11 ID 00 01

- O-AECD 1=ABCP

3=ABC

it=ABC

5=/\BC

6= ABC

2=IBC

8= Ad

9=AV

>-2

Puc. 6.4. Преобразование кода 8421 в десятичные цифры:

а) минимизация функций; б) реализация схемы на элементах И-НЕ; е) схема на элементах И-НЕ с меньшим числом шходов