двух входных переменных, требуется также функция переноса С. В связи с возможностью широкого применения они выпускаются также в виде монолитных интегральных схем.

Одноразрядные полные сумматоры

На рис. 5.34а показана комбинационная таблица полного .одноразрядного сумматора, отличающегося от неполного тем, что он имеет три входа. На выходе S имеется результат сложения двух одноразрядных цифр - Л и В - и переноса Ci предыдущего

S=ABCi+ABCi+ABCi +1601= =A[B®Ci)+Ud®Ci)= =A®B®Ci

Co=tB+CiA+CiB= =Adi-Ci(A+B)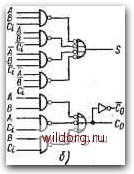

Ci-A

-So -Co

Puc. 534 Полный одноразрядный сумматор:

a) комбинационная таблица и минимизация выходных функций; б) двухуровневая схема сумматора на элементах И-НЕ с использованием дополнений входных переменных; в) схема с неполными сумматорами

сумматора; перенос, который при этом возникает, подается на выход Со и следующий сумматор. Из карт на рис. 5.34 видно, что возможна минимизация только функции Со. Но для составления схемы сумматора могут быть использованы и частично минимизированные функции или с различ1ными алгебраическими преобразованиями, например:

S=ABCi+ABCt+ABCi+ABCi=Ci{AB+AB)+Ci{AB+AB), (5.4)

S==ABCi+ABCi+ABCt+ABCi=Ci{AB+AB)+Ci{AB+AB), (5-5)

Co=ABCi+ABCi+ABCi+ABCi==AB+Ci{AB+AB)==AB+Ct{A+B).{5.6)

Со=ABCi +АВС, +ABCi +ABCi = ЛВ+Сг(ЛВ+ЛБ) = AB+С-(Л+B). (5.7)

На рис. 5.346 имеется пример схемы полного сумматора, составленной на основе алгебраического выражения функции S

(5.4) и преобразоващного выражения функции Со (5.6). Лог»--ка - двухуровневая, что является выгодным с точки зрения уменьшения задержки распространения сигнала, однако необходимы дополнения входных переменных А. В и Ci. На рис. 5.34 представлен полный сумматор, составленный из двух неполных сумматоров и схемы И-НЕ.

Другие примеры схем без дополнений входных переменных даны на рис. 5.35. В схеме на рнс. 5.35а для реализации суммы S©

1 ABCi

ABCi

При объединении дыха- -двВ 1,2,3 на общем Вы-ходе будет функция

\ABCi ABCi

AB+CifAB+АВ)

Рис. 5.35. Примеры схем полных сумматоров:

а) на элементах И-НЕ с двумя и тремя входами;

б) на элементах с двумя входами

-т-1-d

Со

необходима четырехуровневая логика, а для переноса Со - трехуровневая. В более простой схеме на рис. 5.356 для So нужна: шестиуровневая логика, а для Со - пятиуровневая. Без использования логики на объединенных выходах число уровней логикш, было бы еще больше. Поэтому прн использовании основных схем с минимальным числом входов (в рассмотренных примерах схем-И-НЕ) нужно ожидать большее значение задержки распространения сигнала.

На рис. 5.36 показаны примеры схем полных сумматоров, рекомендуемых для случая, когда имеются дополнения входных пе-

(ab+abJcl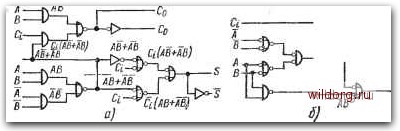

АВт(АВ+АВ]С1.

Рис. 5.36. Примеры схем полных сумматоров с использованием дшошгений входных переменных:

с) на элементах И/ИЛИ-НЕ; б) на элемедтах И/ИЛИ-НЕ и И-НЕ.

с 129

ременных. В схеме на рис. 5.36а использованы базовые элементы И/ИЛИ-НЕ и инверторы, а на рис. 5.366 - комбинация элементов И/ИЛИ-НЕ и И-НЕ. Обратим внимание, что здесь нет необходимости в дополнении входной переменной d.

В рассмотренных сумматорах сигналы проходят через большое число логических ступеней, что вызывает большую их задержку. Каж будет показано далее, при параллельном включении сумматоров результирующая сумма хотя и возникает на параллельных выходах, но неодновременно, так как она зависит 9т отдельных переносов, выполняемых сумматорами последовательно. Поэтому при наличии большого числа сумматоров общая задержка суммы зависит прежде всего от задержки функции С. С точки зрения минимальной задержки выгодны алгебраические формы функций:

(5.8)

Со = AB+ACi+BCi,

(5.9)

которые используются при создании монолитных интегральных сумматоров (примеры схем см. на рис. 5.37, сумматор на рис. 5.37а размещен в одном корпусе). Для обеспечения возмож-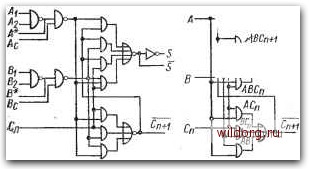

JL l i

А в Сп CntfS S

j> j, f,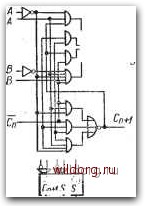

А ВСп Cru-lS S

A в Сп CnilS S

г-гт

Ш£1

А В Сп СпнЗ S

т-гт

Рис. 5.37. а) Полный интегральный сумматор фирмы TI; б), в) дуальные интегральные сумматоры фирмы SGS

НОСТИ прямого соединения входа и выхода переноса С между отдельными сумматорами входы А и В рассчитаны так, что входные переменные могут подаваться на собственный сумматор без инверсии или с инверсией. Такое подключение входов обеспечивает также любое запрещение входных переменных. На рис. 5.376 130