р\(7С О/ 10

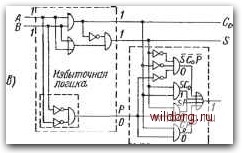ОшиНка.

Логическая схема

Обнаружение оишбон

Рис. 5.56. Определение ошибки в неполном сумматоре:

а) неполный сумматор и его комбинационная таблица;

б) комбинационная таблица и минимизация функции обнаружения ошибки; в) пример схемы обнаружения ошибки

зана на рис. 5.56в. Формирователь сигнала четности Р должев быть независимым от основной логической схемы и поэтому представляет избыточную цепь. Так как у неполного сумматора не может быть одновременно 5 = 1 и Со=1, то схемное решение детектора упрощается Этот принцип может быть использован и в-случае полного сумматора (рис. 5.57). Здесь уже соотношение числа элементов основной логической схемы и контрольных цепей более удовлетворительно.

Для контроля многоразрядных сумматоров можно использовать несколько разных принципов. На рис. 5.58а показана схема-четырехразрядного сумматора, где использован классический, принцип дублирования переноса и контроля четности. Сравнение

" Изложенный метод контроля применительно к схеме рис. 5.56 не можег обеспечить выявление всех ошибок за счет одиночных неисправностей, так как в схеме имеется элемент Hi, участвующий в формировании как Со, так и S. Действительно, прн . = 1, В=1 ошибочное значение Со=0 влечет за собо& ошибочное 5=1, и ошибки не обнаруживаются. (Прим. ред.).

Рис. 5.57. Пример схемы полного одноразрядного сумматора с обнаружением ошибок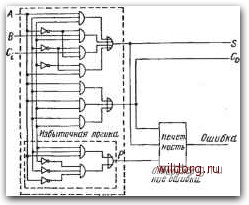

Логи11есмя схема.

Полный, сумматор

Bhs

2<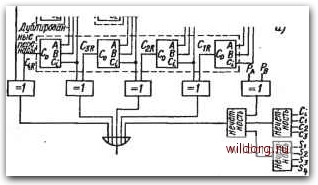

Ошибка

111111 i 111

Нечетность

Ошибка

Рис. 5.58. Пример схемы четырехразрядного сумматора с дублированием переноса:

а) с контролем четности; б) другой возможный принцип контроля

переносов дублированных цепей и контроль четности позволяют обнаружить все ошибки, которые могут иметь место. Другой принцип контроля показан на рис. 5.586. В обоих случаях Ра - четность переменных Ai-At и Рв - четность переменных Bi-В.

Резервирование

Для увеличения надежности может быть использовано резервирование на различных функциональных уровнях, но нужно отметить, что при этом значительно повышается количество базовых элементов. На рис. 5.59а показан пример трехкратного резер-

А Со ЦВ5

1 ГГГГ

Основная логическая схема

I \Нт11рита(1нае\ Гч Wenb I

- мажолё I таотяиепь J

Дешифратор

Со

Рис. 5.59. а) Пример трехкратного резервирования на уровне неполных сумматоров; б) неполный сумматор с трехкратным резервированием на уровне базовых элементов

Мажоритарная цепь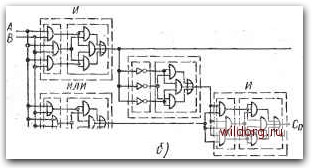

вирова.ния на уровне неполных сумматоров. Дешифраторы выходов S и су представляют собой мажоритарные цепи, принцин действия которых был рассмотрен в § 1.10. На рис.-5.596 представлен неполный сумматор с трехкратным резервированием на уровне базовых элементов И, ИЛИ, НЕ в соответствии со схемой рис. 5.56а: Выходы утроенных базовых элементов объединяют мажоритарные цепи). Такие же принципы могут быть использованы в схемах.с полными сумматорами.

Увеличение надеж-ности может быть обеспечено при условии, если надежность мажоритарной схемы (содержащей четыре элемента) существенно вьняе надежности резервируемого элемента. (Прим. ред.).