=Uii.B=Uu. Последовательность определения сходимости уровней в цепочке схем такая же, как «а рис. 1.21а. При амплитуде сигналов помех Ui,= Ui уровни нечетных схем стремятся к точке F, а уровни четных схем - к рабочей точке D. При увеличении амплитуды сигналов помех до величины f/пг происходит стягивание в рабочие точки / и G и состояние каскада изменяется. Максимально допустимое значение сигнала помех Un определяется в этом случае.

®вГ- %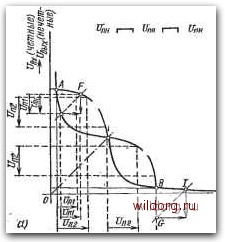

-eulfpx) "четные

ЩЛвчетныв)

-UgjmdmHbid) и(че1гшые)

Рис. 1.22. а) Рабочие условия при наличии помех на всех входах цепочки инвертирующих схем с усилением; б) максимально допустимые значения сигналов помех

согласно рис. 1.226, стороной квадрата, диагональ которого равна максимальной ширине петли в направлении оси 1/вы1=£/в1.

Анализ влияния помех на цепочку неинв€1ртирук>щих схем с усилением проводится так же. На рнс. 1.23 показан пример влияния искажений входных

4lH [-1 пи

-"ф- 1 47)- 2

пн\-I Щн\-I Щ(

ЧТЯ-?-®- * -Ф™ .

Рис. 1.23. Рабочие условия при искажении всех входов в цепочке неин-вертирующих схем с усилением

уровней всех схем цепочки. В отличие от инвертирующих схем, здесь уровня Н и В не зависят друг от друга, так как все схемы находятся в состоянии В или Н. Поэтому при искажении уровня Н предполагаем наличие сигнала [/д.н на входах всех схем, при искажении уровня В - сигнала [/ц.в на входах всех схем. Так как петли, образуемые передаточными характеристиками, неодинаковы, то отличаются друг от друга и значения максимально допустимых сигналов помех Un.n и f/п.в-

Определение допустимого уровня статических помех

На рис. 1-24 определены максимально допустимые пределы помех на основе .надежной сходимости уровней в цепочке схем и с учетом максимально возможного разброса передаточных характеристик соответствующих схем.

Собственные пределы искажений ПС на практике большого значения не имеют, так как они справедливы только в случае искажения в одной схеме цепочки.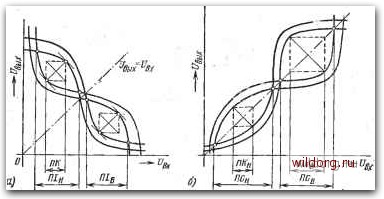

Рис. 1.24. Определение собственных в цепочке схем пределов помех: а) инвертирующей схемы с усилением; б) неинвертирующей схемы с усилением

С точки зрения практического расчета систем большее значение имеют пределы помех ПК, допустимые для системы схем. У инвертирующих схем абсолютное значение ПК для состояний Н и В одинаково, но для состояния Н это положительное искажение, а для состояния В - отрицательное. У неинвертирующих схем с усилением нужно различать две величины: положительный уровень ПКн и отрицательный уровень ПКв.

На основе представленного выше материала можно определить также пределы допустимых помех в случае наличия их на входе каждой нечетной схемь* в цепочке. Эта величина имеет ограниченное значение и может быть использована прн расчетах некоторых несложных бистабильных схем.

Другой способ нахождения пределов величин статических помех основан на определении так называемых переходных точек, связанных с изменением крутизны передаточной характеристики при перемещении рабочей точки из состояния Н в состояние В и наоборот. Обычно онн определяются как точки с усилением, равным единице. У инвертирующих схем это точки на передаточной характеристике, которым соответствует А[вых/Авх=--1; у неинвертирующих схем с усилением- А1/вых/А1/бх=1. Такое определение предполагает наличие почти .ядеальиой передаточной хара1ктер.ист.ики с большим .изменением крутизны между состояниями Н и В. В противном случае получаемые пределы помех не будут точны и не обязательно будут иметь связь с надежной сходимостью уровня. На рис. 1.25а даны примеры определения пределов помех

-ПП для двух вцдов передаточных характеристик - А и В. УровевБ помех ППн одинаков для характеристик А и В, хотя видно, что схема с характернетикок А имеет больший системный уровень помех ПК, чем схема с характеристикой В.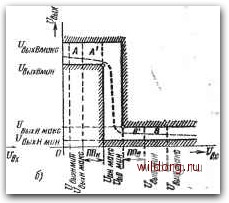

Рис. 1.25. Определение пределов помех, основанное:

а) на переходных точках, б) на гарантированных напряжеввях

Еще одно оп)ределеине пределов величин помех осяовано на гарантирован-иых напряжениях в случае самых тяжелых рабочих условий (рие. 1.256). При эвходиом напряжении С/вхНыаке гарантируется минимальное выходвое напряжение {выхвмип. а при входном напряжении [/вхВмия обеспечивается максимальное выходное напряженке £/выхнмакс- В этом случае пределы помех будут:

(1.8> (1.9)

Рабочие точки схемы в установивщемся режиме могут быть в облаети А или В, .влияние вомех включает область А ил!г В.

- вхН макс "~ »ьжН макс, = вьис В мин ~~ вхВ мин-

Пределы допустимых кратковременных помех цифровых схем

Статические помехи представляют собой с точки зрения искажений самы& тяжелый случай. Однако помехи, возникающие в электронной системе, имеют преимущественно другой импульсный характер: от импульсов произвольной формы и сравнительно большой длительности до кратковременных иглообразных импульсов. Так как этот тип помех, обусловленный, главным образом, ем-костэдыми связями, ограничивает скорость переключения цифровой сиетемы, то при ишользовании быстродействующих схем, овобеиио интегральных, необходимо знать допустимые пределы кратковременных помех.

Принцип несложного и точного метода определения пределов кратковременных помех иллюстрируется рис. 1.26. Инвертирующая схема А, в которой проводятся измерения, имеет два входа: на одном - постоянно имеется уровень В, а на второй--подаются имитированные импульсы помех с различными амплитудой н длительностью. Схемы В и С того же типа, что и схема А, они включены так, что составляют простую бистабильную схему, являющук>ся индикатором изменения состояния схемы А под дейстаием импульса помех.

Рассмотрим сначала искажение уровня Н схемы А. В нормальном состоя--нии без помех на выходе схемы А имеется уровень В, иа выходе ехемы В - уровень Н и на выходе схемы С -уровень В. Предположим теперь, что на входной уровень Н схемы А воздействует идеальный положительный импульс, в результате чего выходной уровень схемы А нзмеиитея по истечении времени