одинаковую функцию при использовании базовых элементов И-НЕ и ИЛИ-НЕ, но задержка распространения больше, чем в схеме контроля нечетности. Примеры пирамид контроля нечетности различного числа бит показаны на рис. 5.25е.

На рис. 5.26а показан пример схемы контроля нечетности трех бит, которая состоит из базовых цепей И-НЕ и ИЛИ-НЕ. Пример использования этих цепей для контроля нечетности двенадцати -бит представлен на рис. 5.266. При использовании типовых интег-

ИЛИ-НЕ И-НЕ И-НЕ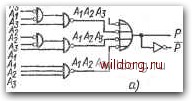

U-L J U JJJl

™1 IHevewi [нечет-Ы \,носгъ\ \ носг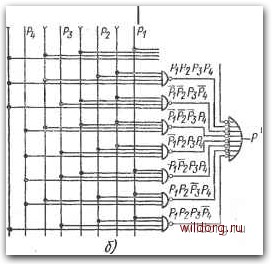

Рис. 5.26. а) Схема контроля нечетности трех бит, составленная из базовых элементов И-НЕ и ИЛИ-НЕ; б) схема контроля нечетности двенадцати бит

ральиых схем для реализации схемы необходимо 15 корпусов.

На рис. 5.27 показан пример схемы контроля восьми бит в базисе ИЛИ-НЕ. Обратим внимание на упорядочение базовых схем, которое позволяет уменьшить число уровней логики, а значит, уменьшить и результирующую задержку распространения. Схему можно рекомендовать для случая, когда имеются дополнения входных переменных.

На рис. 5.28а, б - схемы контроля-двух и трех бит с дополняющими входными переменными. Это - базовые элементы типа 122

Рис. 5.27. Схема контроля четности восьми бит, составленная из элементов ИЛИ-НЕ

А2

Четность

нечетность

А2-\Г\

2

Аг-Аг-

. /15-

13 A,.

" Ai

/Is-j £ /1б

7- g

/17-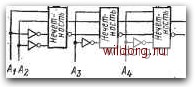

Puc. 5.28. a), 6) Схемы контроля четности двух и трех бит с использованием дополняющих входных переменных; в) примеры схем контроля четности семи переменных; г) пример итеративной схемы контроля четности п бит

И/ИЛИ-НЕ. Схемы на рис. 5.28е предназначены для контроля семи бит.

До сих пор мы рассматривали пирамидальное построение контрольных схем. Если большая задержка распространения не имеет существенного значения, то для контроля .четности может быть использована сравнительно простая последовательная (итератив-, пая) схема, представленная на рис. 5.28г.

5.7. ПОРОГОВЫЕ ЦЕПИ И ДЕТЕКТОРЫ m ИЗ п

Для контроля различных кодов m из п или кодов, заданных комбинацией входных переменных, можно использовать так называемые детекторы т из п, принцип действия которых основан на использовании пороговых цепей. Общий принцип детектора т из п показан на рис. 5.29а. В схеме использованы две пороговые

f-m

т=1

>2

Рис. 5.29. а) Принцип действия детектора т из п; б) принцип действия детектора 1 из п

цепи, обозначенные m и т+1. На выходе пороговой цепи т будет 1 только тогда, когда 1 имеется на т иш больше входах из общего числа п входов. На выходе пороговой цепи т+1 будет 1 только тогда, когда она есть на m-f 1 или больше входах из общего числа п входов. Из сказанного следует, что на выходе F будет 1 только тогда, когда 1 имеется точно на т входах, так как в этом случае будет 1 на выходе цепи m и О на выходе цепи т+1. Выход F=0 означает ошибку, т. е. число единиц на входах больше или меньше т. Сравнительно прост детектор 1 из п, представленный на рис. 5.296. В этом случае функцию пороговой цепи т выполняет базовый элемент ИЛИ, на выходе которого имеется 1, если на одном или более входах есть 1.

Описанный принцип может быть использован и для большого числа входов п. Детекторы m из п для малого числа входов п магут быть составлены, исходя прямо из алгебраического выражения требуемой выходной функции. На рис. 5.30а имеется пример схемы детектора 1 из 4, на рис. 5.306 - схемы детектора 2 из 4, а на рис. б.ЗОе- детектора 3 из 4. При составлении схемы должны быть рассмотрены все возможные комбинации входных переменных.

Пороговые цепи 2 из п для любого числа входов можно составлять так, как это показано на рис. 5.31а на примере порого-