Если обозначить выходы двоичнозакодированных десятичных цифр, единичной декады /4/3/2/1 я десятичной декады DfDsDDi, то умножение на соответствующую степень числа 2 будет получено размещением значений / и D на соответствующие позиции, отвечающие указанной сумме. На практике это означает подачу бят /4/3/2/1 и DiD3D2Di на одноразрядные полные сумматоры, размещение которых соответствует указанной сумме. Пример схемы можно видеть на рис. 5.51а размещение сумматоров соответству-

\CdSS I

/ е Ci

CoSS

А В С,

А В Ci\ CoSS

D2J3

- в а\

CoSS

ABCi CoSS

I в Ci CoSS

1 70

Puc. 5.51. Схема преобразования двоичнокоди-рованных десятичных чисел в двоичную систему

2f2 ZZ ZZ"

ет схеме на рис. 5.516. Если не важна величина задержки, то рассмотренный принцип может быть использован для преобразования любого числа декад.

А2В2 AfBi

Ш Ш

Г LSTY

А В СП

CoSS

А,,Вц А3В2 hz f/

\A В Ci

A В Ci .CoSS

urn?

A BCi

CoSS

A BCi

CoSS

fst\ [ssU tstU rfSj

-АуВ

B5A5 Be As в>A BgAs

Puc. 5.52. a) Сравнение четырех иеремеи-ных; б) восьми переменных

На рис. 5.52а показана схема несложной цепи сравнения переменных и Б4В3В2В1. Основой схемы является параллельный вычитатель. При С,-=1 единица имеется одновременно на всех входах цепи оценки И-НЕ, если А=В. На рис. 5.526 прше-дена схема, произ1водящая сравнение восьмиразрядных чисел. В этой схеме вход Q первого сумматора имеет постоянное значение 0. ,

Нетность

Одноразрядные полные сумматоры могут использоваться в схемах генерирования сигнала четности или контроля четности. На рис. 5.53а в качестве генератора сигнала четности трех бит используется сумматор. Генератор сигнала четности четырех бит с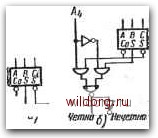

Мечетно- Уетно

рей!

\CoS s

CoSS

[A BCi\

A В Ci CoSS

Puc. 5.53. a) Полный одноразрядный сумматор как генератор четности трех бит; б) генератор четности четырех бит; в) генератор четности девяти бит с дуальными сумматорами

дополнительной схемой И/ИЛИ-НЕ показан на рис. 5.536, на рис. 5.53в - генератор сигнала четности девяти бит, построенный с дуальными сумматорами. Представленные схемы, естественно, -•могут быть использованы и для контроля четности.

в Ci. CqSS

Л4 А2 At

А BCi CoSS

А в Ci

CpSS

Р, Р2 Ад Рз А,,А2А,

Ъ Рг Рз fhN

Генератор \Шт четтт \четш\ [четтстЛ

Pi PzWi?!

/I в Ci CoSS

А в Ci CpSS

А в Сц

CoSS\

й BCi CoSS

\CoSS

А BCi CoSS

Рис. 5.54. a) Генератор трех бит четности семиразрядного кода Хэм-минга; б) схема обнаружения места сшибки, использующая дуальные сумматоры; в) схема обнаружения места ошибки, использующая генераторы четности

Использование полных сумматоров удобно также для формирования кодов Хэмминга, обнаружения и исправления ошибок, принцип которых рассмотрен в § 3.3. На рис. 5.54а представлена построенная на трех сумматорах схема, предназначенная для формирования проверочных символов Р1Р2Р3 семиразрядного кода Хэмминга. Переменные ЛвЛИгЛх представляют число в обычном двоичном коде 8421. На рис. 5.546 показана схема с дуальны-

/ о 1 о

о о Ps

Правильный D D 1 1 перенос (Т)0 1 1 Неправильный AsAA2/i, перенос

Адрес неправильной цифры

J!l=P2®As®A2®Ari Л2=Рз®А®А2®Аг О

Дешифратор адреса

О О

Исправление неправильного /\f переноса

Рис. 5.55. Структурная схема устройства обнаружения места и исправления ошибки

МИ сумматорами, предназначенная для обнаружения места ошибки. Такую же функцию имеет схема на рис. 5.54в, где место ошибки определяют три четырехразрядных генератора четности. Рисунок 5.55 показывает общую структурную схему обнаружения места ошибки и ее исправления.

Обнаружение ошибок в сумматорах .

Простой способ обнаружения ошибок состоит в контроле на четность кода с одним проверочным символом. Рассмотрим сначала неполный сумматор, комбинационная таблица которого дана на рис. 5.56а. Кроме выходов 5 и Со, рассмотрим также выход для сигнала четности, который имеет значение 1 только тогда, когда одновременно Л = 0 и B = Q, т. е. правильные выходы 5СоР всегда удовлетворяют условию нечетности. Обнаружение четности при контроле этих выходов означает наличие ошибки. Алгебраическое выражение, определяющее ошибку, находится с помощью комбинационной таблицы и карты на рис. 5.566. Результирующая схема неполного сумматора с контролем четности пока-