6.12. СРАВНЕНИЕ

Синтез схемы сравнения последовательных информационных сигналов представлен на рис. 6.148. Предположим, что сравниваются два п-разрядных двоичных числе - А и В, у которых сначала сравниваются младшие разряды. Диаграмма состояний и таблица состояний для требуемой функции представлены на рис. 6.148а. Входные переменные обозначены Л и В, а внутренние переменные X и У. Перед сравнением младших цифр внутренние переменные имеют значения X=Q, У=0. Если в следующий момент А>В, то Х=1 и У=0, если В>А, то Х=0 и У=1, если Л = Б, то состояние не меняется. Неиспользованное состояние Х=1, У=1 можно использовать для упрощения логической функции. На основе комбинационной таблицы или карты переходов составляем программные карты входов - рис. 6.1486. Допустим, что будут использованы (-триггеры. После определения алгебраических выражений логических функций входов JK можно составить схему на выбранных базовых элементах. На рис. 6.153в показана схема с элементами ИЛИ-НЕ. После сравнения старших разрядов один из трех выходов имеет значение 1 ё зависимости от того, если А>В, В>А или А=В.

6.13. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ Сложение и вычитание двоичных чисел

Для сложения двоичных чисел можно использовать простой последовательный сумматор, схема которого показана на рис. 6.149. Таблица состояний на рис. 6.149 составляется на основе правил арифметического сложения. Из таблицы следует, что схема должна иметь одну внутреннюю переменную, а значит, и один триггер. По таблице состояний на рис. 6.1496 составлены карта внутренней переменной У, соответствующая требуемым переносам при сложении, программная карта входов С-триггера и карта выхода S, на котором появляется результат сложения. Результирующая схема на логических элементах И/ИЛИ-НЕ показана на рис. 6.149в. Очевидно, что последовательный сумматор состоит, в принципе, из полного одноразрядного сумматора и из триггера, записывающего перенос, который возникает при сложении двух двоичных цифр. Последовательный синхронный сумматор имеет два входа --Ли В, на которые последовательно подаются два суммируемых двоичных числа, вход тактовых импульсов ТИ и только один выход S. Составление схемы асинхронного сумматора с динамическим асинхронным триггером производится так же.

Принцип сложения двух двоичных чисел - Л и Б - показан на рис. 6.150а. Здесь представлена последовательная запись обоих чисел в сдвиговые регистры Л и В. Перед записью D-триггер находится в состоянии Q=0, а управляющие входы сдвиговых регистров устанавливаются в положение Х=\, У=1. Двоичное число

АВ /\ О 1

В-Т.

)KQ.

у+АВ+АВ Ги+ЛЕ+АВ

l---b-\±JBABU

JyfY

Jy=AB;l<y=AB

у+ЛВ+АВ

уШ-ГВ) s=y(fil*AB)*y(AB*M) S=y(AB*AB)-y(AB*AB)

S

у{АВ+Ав)

Рис. 6.149. Последовательный двоичный сумматор:

а) таблица состояний; б) карта функций У, карта функции S н программная карта входов /, /Г; е) схема сумматора на логических элементах,И/ИЛИ-НЕ

ти- ТИ .

в о -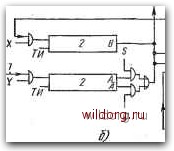

Рис. 6.150. а) Принцип сложения двух двоичных чисел - А и В; б) принцип сложения и вычитания двух двоичных чисел- А и В; 1 - последовательный ввод; 2 - сдвиговый регистр; 3 - последовательный вывод

в, имеющее п разрядов, после п тактовых импульсЪв оказывается записанным в сдвиговый регистр А, а так как Q=0, то после следующих п тактовых импульсов оно через полный одноразрядный сумматор (с его выхода S) будет записано в сдвиговый регистр В Одновременно на освобождающиеся места сдвигового регистра А записываются разряды двоичного числа А. Таким образом, для записи обоих.чисел необходимо 2п тактовых импульсов. После записи управляющие входы сдвиговых регистров устанавливаются в положение Х=\, У=0. При первом тактовом импульсе младшие разряды чисел перемещаются в полный сумматор. В результате этого сдвига освобождаются старшие разряды (слева) обоих регистров. Результат сложения с выхода S сумматора переносится на освободившееся слева место в сдвиговом регистре В, перенос записывается в триггер и т. д. По окончании сложения управляющие входы обоих регистров устанавливаются в положения Х=0, У=0, а результат сложения может быть выдан из регистра В в последовательной форме. Для ускорения операции можно использовать особый сдвиговый регистр, записывающий результирующую сумму или производящий параллельную запись или передачу информации из сдвиговых регистров. Схема на рис. 6.1506 позволяет производить сложение и вычитание двоичных чисел.

Сложение и вычитание двоичных кодов десятичных цифр

Для сложения двоичных кодов десятичных цифр могут быть использованы интегральные четырехразрядные параллельные сумматоры. Основная схема показана на рис. 6.151. Перед суммиро-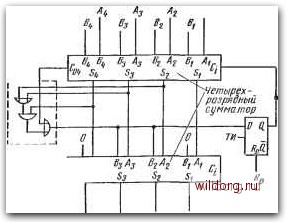

Выявление поправки и Bl Al переноса - Сд

Рис. 6.151. Сложение двоичных кодов десятичных цифр

ванием триггер типа D установится асинхронным входом в состояние Q=0. Двоичные коды десятичных цифр Л и В с выходов сдвиговых регистров суммируются в первом четырехразрядном