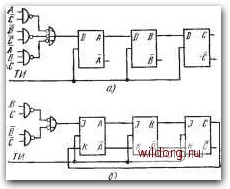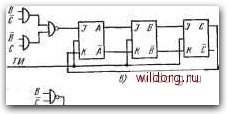Рис. 6.126. Сдвиговые регистры с ОС, имеющие цикл иа рис. 6.124а: а) на /Э-триггерах; б), в), г) на Ж-триггерах

числа каскадов п регистра, так как является функцией состояния всех п каскадов. Значительно проще сдвиговые регистры с ОС, имеющие длину цикла L=2"-I.

Сдвиговые регистры с обратными связями, имеющие длину цикла 2"-1

Периодический цикл этих регистров имеет максимальную длину L=2"-I и обозначается как цикл максимальной последовательности М. Последовательности М длиной 2"-I возникают при использовании таких обратных связей, которые можно выразить в форме суммы по модулю 2, т. е.

S=aiA@a2B@cij::®aJ)® . . ., (6.И)

где Gi, С2, Сз, С4... равны О или I. Состояние 0000 ... О не включено в циклический код, соответствующий последовательности М.

На рис. 6.126 приведены пример для случая n=3 и функции обратной связи в виде F=A®C, L = 2-1=7. Аналогично можно получить схему с функцией ОС в виде F=B®C. На рис. 6.126в показан пример реализации схемы на D-триггерах. Такая же логическая схема с инверсией может быть использована в схеме на (-триггерах (рис. 6.126г). Однако сравнение функции F с характеристическим уравнением /Д-триггера показывает, что схему можно очень легко реализовать так, как это сделано на рис. 6.126d. Если теперь обратить внимание на диаграмму состояний на рис. 6.126с, то очевидно, что состояние ООО не включено в циклический код. Если схема находится в этом состоянии, то ее работа будет блокирована. Из этого заблокированного состояния схема будет переключена в требуемый цикл только тогда, когда одна из переменных-А, В, С - изменит свое состояние с О на 1, причем или после внешнего воздействия, например установкой одного из триггеров в состояние 1 с помощью вспомогательного входа, или 278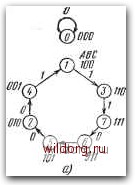

А 00 О! II 10

1 Т)

(ТТ)

F=AC+A[:=>J=C;K=C ВС

А =А=

А -> с -V

Рис. 6.126. Сдвиговый регистр с ОС, имеющий длину цикла !L=7: а) основной цикл; б) определение функции ОС и программная карта входов-- С-Триггера; в) схема на Й-триггерах; г), д) схемы на /iC-Tpnrrepax

автоматически. Автоматическую установку нужного цикла необходимо решать уже с учетом функции обратной связи F; это, естественно, требует более сложной логической схемы. Пример решения приведен на рис. 6.127.

Рис. 6.127. Синтез сдвигового регистра с ОС, имеющего iL = 7 с автоматической установкой нужного цикла

АСАС* А ВС

илиЕ=АС+.АС-АВ=АС-А(,В-С} ВС

А 00 01 11 10 О

Вд=С

Схема с логикой, обеспечивающей установку нужного цикла,, представлена на рис. 6.128с. Схема может быть использована как генератор циклического кода (см. рис. 6.127) или как счетчик. Во-втором случае на выходе нужна дополнительная логическая схе-

Выход

BC-0 -

D В В

2? C-C -

КС--

Рис. 6.128. Примеры схем сдвиговых регистров с ОС {L=7) с автоматической установкой нужного цикла (см. рис. 6.127):

а) с логической схемой на входе регистра; б) с вспомогательной логической схемой на установочном входе S входного триггера; в) с логической схемой на входе регистра

Таблица 6.4. Функции ОС без автоматической установки цикла