нал R или S может иметь значение 1 или О, как это следует из пунктирных зависимостей на временной диаграмме.

Используя сокращенные таблицы развития, составляем карты (рис. 6.30) и определяем простейшие алгебраические выражения функций Yi и Yz. Результирующая схема на элементах ИЛИ-НЕ и базовом S-триггере (ИЛИ-НЕ) показана на рис. 6.306.

У1у\оо 01 а ю 00 01 н 10 оо oi н ю оо oi и ю

00 01

У1=У1Т+У2Т01 , 5=у,

Y2y2J+yiiBj ,-R=yz

Yj = T+yiy2+yiQl У2=Т+уф+У2а1

01010

rOIOD

l--t>o-

yi*Qi 00010

У1+У2

Lj>o-

01000

01000\

i>°-boiDi I moid

У1+У2

10001

У2+Ч1

Триггер ИЛИ-НЕ

1 10011

101100 J-Ql

Yi=T(y,+y2)(y,+Qi)

У2-Т(у,+У2)1у2Щ)

Рис. 6.30. Синтез Г-триггера, основанный на использовании JS-триггера:

а) карты; б) схема с iRS-триггерами ИЛИ-НЕ

Асинхронные импульсные триггеры с непосредственными связями

Из примеров, приведенных в предыдущих главах, вытекает, что на выход асинхронного триггера после определенной задержки непосредо-твенно воздействует положительное или отрицательное изменение сигналов на управляющих входах. При решении предполагалось, что управляющие сигналы имеют активное положительное изменение из состояния покоя О в состояние 1 и пассивное отрицательное изменение со значения 1 назад к значению О, как это показано на временной диаграмме рис. 6.31с. Выход изменяется непосредственно после положительного изменения сигнала на соответствующем управляющем входе. Ко всем триггерам,

.4» 18

рассмотренным в предыдущих параграфах, можно составить инверсные триггеры, для которых значение управляющих сигналов в состоянии покоя равно 1, как это показано на рис. 6.316. В этом

Состояние покоя Состояние поШ

J-~L

г)

Рис. 6.31.. Активные изменения сигналов на управляющих входах, оказывающие влияние на состояние выходов:

а, б) статических; в, г) динамических асинхронных триггеров

случае состояние выхода изменится непосредственно после активного отрицательного изменения управляющего сигнала. Но существует еще другая возможность составления асинхронных триггеров на основе временных диаграмм рис. 6.31в, г. С точки зрения управления входами их функция аналогична динамическим триггерам с импульсными входами, которые реагируют только на спад управляющих импульсов. Приведем примеры схем на основе временной диаграммы на рис. 6.31в.

О Ф ф Ф® ф ф ©ф ф Ф

d е f

01 11 10

01 01 10 10

00 01

77 W

© i5 - ®

"01 A

01 В

10 с

DO A

Puc. 6.32. Синтез динамического JS-триггера: a) временная диаграмма; б) примитивная таблица развития; в) сокращенная таблица и соответствие внутренних переменных

RS-триггер. Как видно из временной диаграммы на рис. 6.320 число устойчивых состояний здесь больше, чем у простого базово- го ?5-триггера, составленного из двух элементов ИЛИ-НЕ.

Из карты развития на рис. 6.33а следует, что возможно несколько решений схемы в зависимости от того, какие значения

уу\ 00 01 11 10 00 01 11 10 00 01 то 00 01 11 1о\о,02

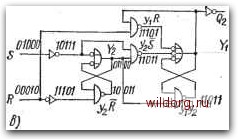00110 Qi

Puc. 6.33. Динамический JJS-трнггер:

a) карты; 6) схема на элементах И-НЕ;

представление схемы «б»

в) другое

Yz будут соответствовать неспецифицированным состояниям Результатом одного варианта решения, показанного в карте функ- Ций Yi, Уг, является схема на рис. 6.336, реализованная на элементах И-НЕ. Та же схема в более наглядном виде представлена на рис. б.ЗЗв.

На рис. 6.34 показана последовательность составления сиМ метричной схемы с использованием двух базовых /?5-триггеров.. Результирующие схемы не только более наглядны, но и более-просты, при этом особенно видна разница в использовании эле* ментов ИЛИ-НЕ и И-НЕ.