
 |
|
Главная страница Дискретный канал связи [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [ 139 ] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] Серии принятых Битое Р8гуяирующий буфер  АйрБснйя логика йекоВироеания -© Рис. 12.14. Декодер для (12, 9)-кода Вайнера-Эша.
Рис. 12.15. Таблица декодирования для (12, 9)-кода Вайнера-Эша. 2) ИЗ регистра синдрома вычитается корректирующий синдром. Первый вариант характерен для кодов, исправляющих одну ошибку. Изучим второй вариант на более сложном примере. Регулирующий Буфер Проверка на наличие оЗного из слеВующих синВромов!/ 0 0 111 0 110 1 0 0 0 10 110 11 0 10 0 1 10 0 11 Серии принятых битое -(+М+) Проверка на наличие оВиого из слеВующих cuHSpoMoe.v 0 0 10 1 0 1111 0 0 0 10 0 10 11 110 0 1 10 0 0 1 Рис. !g.I6. Декодер для сверточного (6, 3)-кода.  Конфигурация ошибок.. СинВром
Рис. 12.17. Таблица декодирования для сверточного (6, 3)-кода. На рис. 12.3 был представлен кодер для (6,3)-кода, исправляющего двойные ошибки. Соответствующий декодер изображен на рис. 12.16. Он использует таблицу синдромов, приведенную на рис. 12.17. Кодер исправляет две ошибки в шести первых битах. С помощью обратной связи вклад каждой исправленной ошибки удаляется из регистра синдрома; так как код несистематический, информационные символы восстанавливаются по исправленному Конфигурация ошибок СинЭром
Рис. 12.18. Таблица декодирования для сверточного (12, 6)-кода. Рйзвеление на гарамельные потоки Серии принятых битое 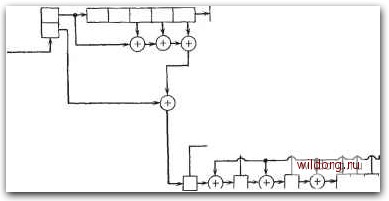 Серии информационных Битов Рис. 12.19. Декодер для сверточного (12, 6)-кода.
[0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [ 139 ] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] 0.0121 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||