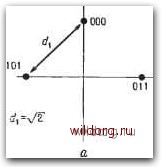• 001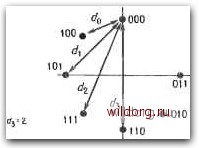

Состояние 00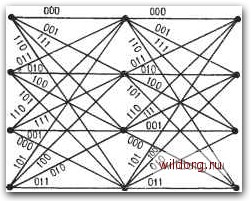

Рис. 15.6. Простой пример кодирования, а - четверичный набор ФТ-модулиро-ваниых сигналов при отсутствии кодирования; б - восьмеричный набор ФТ-модулированных сигналов; в - решетка для сверточного (6, 4)-кода.

Евклидово свободное расстояние , обозначаемое через doo, определяется как минимум евклидовых расстояний всех возможных пар кодовых слов из . Евклидово свободное расстояние является подходящим расстоянием для измерения кодовых характеристик в гауссовском канале. Это следует из того, что в гауссов-ском канале вероятность ошибки асимптотически ) удовлетворяет неравенству

где о - среднеквадратичное отклонение шума, Q - интеграл гауссовского распределения, а Na - число кодовых слов на

1 При о -> 0. - Прим. ред.

расстоянии doo от слова, целиком состоящего из нулей. Следовательно, увеличение doo, грубо говоря, эквивалентно уменьшению 0. Вот почему увеличение свободного расстояния мы называем выигрышем сверточного кода.

Евклидово свободное расстояние часто измеряется в децибелах; эта мера определяется соотношением

doo (дБ) = 20 logio doo.

Асимптотический выигрыш кодирования определяется формулой

G = 20 logio {djdrei),

где dref - минимальное евклидово расстояние между незакоди-рованными соответствующими сигналами той же мощности.

На рис. 15.6 представлен простой пример. Сверточный код определяется восьмеричным набором ФТ-модулированных сигналов и решеткой в кодере. Он представляет собой (6,4)-код со скоростью 2/3. Пример несистематического кодера представлен на рис. 15.7, а. Соответствующий код может также использоваться как систематический, если рассматривать второй и третий биты в каждом кадре как информационные. Однако для реализации кода в систематической форме надо ввести в кодере обратную

Регулирующий Буфер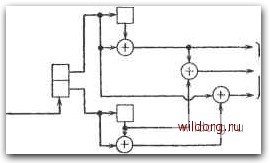

Информационные бипы

К 8-ичному ФТ-моЭуляшору

Регулирующий буфер

К-е-ичному ФТ-мойулятору

Информационные биты

Рис. 15.7. Кодеры для сверточного (6, 4)-кода. с-кодер с регистром сдвига, не использующий обратную связь; б - кодер с регистром сдвига, использующий обратную связь.

Два бита на вхойе

К 8-ичномд ФГ-мовуляглору

cL = c/3 =2,000 Выигрыш е 3 АБ по сравнению с i-ичной ФТ

Два бита на вхойе

Два бита на ехойе

к 8-ичному ШТ-мойулятору

К Б-ичному ФТ-мойулятору

Выигрыш 6 3,6 йБ по сравнению с .-ичной ФТ

Выигрыш в 4,1 ЭБ по сравнению с -ичной- ФТ

Рис. 15.8. Некоторые коды для восьмеричного канала с ФТ-модуляцией.

связь, как показано на рис. 15.7, 6. Символ кодового слова содержит лишь два бита информации, а может принимать восемь различных значений. На рис. 15.6, в легко видеть, что минимальный вес имеет путь 001 011 ООО; ему соответствует кодовое слово, находящееся на минимальном расстоянии от кодового слова,

ео оо ов во оо оо оо оо о оо во оо о» оо оо оо о о «о со оо оо о» оо оо о Запись " * *

ввоичная (ООО) Ц001 (010) (ПО) (001) (101) (011) (ИМ (соссг.) восьмеричная 0 534567