Информационная послейобательность: к битов КобовоЕ слово: п битов Скорость=Л/л

Блоковый коО

Информационная скорость:/рбитов/кайр Скорость канала: Ло Битов/кайр Скорость коОа:Ао/Ло BumoB/ffum

битов/каЗр

Древовибный к,ов Рис. 1.2. Основные классы кодов.

Древовидный код более сложен. Он отображает бесконечную последовательность информационных символов, поступающую со скоростью 0 символов за один интервал времени, в непрерывную последовательность символов кодового слова со скоростью щ символов за одни интервал времени. Мы отложим рассмотрение древовидных кодов до гл. 12 и сначала сосредоточим внимание на блоковых кодах.

Если сообщение состоит из большого числа битов, то в принципе лучше использовать один кодовый блок большой длины, чем последовательность кодовых слов из более короткого кода. Природа статистических флуктуации такова, что случайная конфигурация ошибок обычно имеет вид серии ошибок. Некоторые сегменты этой конфигурации содержат больше среднего числа ошибок, а некоторые меньше. Следовательно, при одной и той же скорости более длинные кодовые слова гораздо менее чувствительны к ошибкам, чем более короткие кодовые слова, но, конечно, соответствующие кодер и декодер могут быть более сложными. Например, предположим, что 1000 информационных битов передаются с помощью (воображаемого) 2000-битового двоичного кода, способного исправлять 100 ошибок. Сравним такую возможность с передачей одновременно 100 битов с помощью 200-битового кода, исправляющего 10 ошибок на блок. Для передачи 1000 битовне-обходимо 10 таких блоков. Вторая схема также может исправлять 100 ошибок, но лишь тогда, когда они распределены частнымоб-разом - по 10 ошибок в 200-битовых подблоках. Первая схема может исправлять 100 ошибок независимо от того, как они рас-

положены внутри 2000-битового кодового слова. Она существенно эффективнее.

Эти эвристические рассуждения можно обосновать теоретически, но здесь мы к этому не стремимся. Мы только хотим обосновать тот факт, что хорошими являются коды с большой длиной блока и что очень хорошими кодами являются коды с очень большой длиной блока. Такие коды может быть очень трудно найти, а будучи найденными, они могут потребовать сложных устройств для реализации операций кодирования и декодирования.

О блоковом коде судят по трем параметрам: длине блока п, информационной длине k и минимальному расстоянию d*. Минимальное расстояние является мерой различия двух наиболее похожих кодовых слов. Минимальное расстояние вводится двумя следующими определениями.

Определение 1.4.2. Расстоянием по Хэммингу между двумя 9-ичными последовательностями х и у длины п называется число позиций, в которых они различны. Это расстояние обозначается через d (х, у).

Например, возьмем х= 10101 и у = 01100; тогда имеем d (10101, 01100) = 3. В качестве другого примера возьмем х = = 30102 и у = 21103; тогда d (30102, 21103) = 3.

Определение 1.4.3. Пусть = jc, t = О..... М - 1) -

код. Тогда мичимальноз расстояние кода равно наименьшему из всех расстояний по Хэммингу между различными парами кодовых слов, т. е.

d* = min d {ci, Cj).

(n, й)-код с минимальным расстоянием d* называется также (п, k, й*)-кодом.

В коде , выбранном в первом примере данного параграфа,

d (10101, 10010) = 3, d (10010, OHIO) - 3,

d(10101, OHIO) = 4, d(10010, 11111) = 3,

d (10101, 11111) = 2, d (OHIO, 11111) = 2;

следовательно, для этого кода d* = 2.

Предположим, что передано кодовое слово и в канале произошла одиночная ошибка. Тогда принятое слово находится на равном 1 расстоянии по Хэммингу от переданного слова. В случае когда расстояние до каждого другого кодового слова больше чем 1, декодер исправит ошибку, если положит, что действительно переданным словом было ближайшее к принятому кодовое слово.

Произвольные л-лослейовательности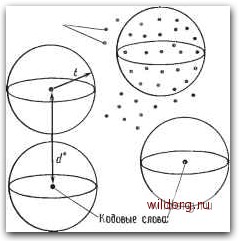

Рис. 1.3. Сферы декодирования.

в более общем случае если произошло t ошибок и если расстояние от принятого слова до каждого другого кодового слова больше то декодер исправит эти ошибки, приняв ближайшее к принятому кодовое слово в качестве действительно переданного. Это всегда будет так, если

d* 2/ + 1.

Иногда удается исправлять конфигурацию из t ошибок даже тогда, когда это неравенство не удовлетворяется. Однако если d*-<2/+ I, то исправление любых t ошибок не может быть гарантировано, так как тогда оно зависит от того, какое слово передавалось и какова была конфигурация из t ошибок внутри блока.

Геометрическая иллюстрация дается на рис. 1.3. В пространстве всех 9-ичных «-последовательностей выбрано некоторое множество п-последовательностей, объявленных кодовыми словами. Если d* - минимальное расстояние этого кода, л t - наибольшее целое число, удовлетворяющее условию d *2/+1, то вокруг каждого кодового слова можно описать непересекающиеся сферы радиуса t. Принятые слова, лежащие внутри сфер, декодируются как кодовое слово, являющееся центром соответствующей сферы. Если произошло не более f ошибок, то принятое слово всегда лежит внутри соответствующей сферы и декодируется правильно.

Некоторые принятые слова, содержащие более t ошибок, попадут внутрь сферы, описанной вокруг другого кодового слова, и будут декодированы неправильно. Другие принятые слова.