Вычисление компонент синйрома

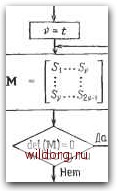Нйхожйениелокаторов ошибок

Д,(/=1.....i)

с помощью вычисления корней Л.г-;

Сш)п

Рис. /.1. Декодер Питерсона-Горенстейиа-Цирлера.

Поскольку число элементов поля конечно, обычно простейшим путем нахождения корней многочлена Л (х) является метод проб и ошибок, известный как процедура Ченя. Эта процедура состоит просто в последовательном вычислении Л (а) для каждого / и проверки полученных значений на нуль. Наиболее простым способом вычисления значения Л (х) в точке 3 является схема Горнера:

Л (3) = (.. .(((Л,3 + Л,. 1) 3 + Л„ ,) 3 +

+ л„ з)р-ь ... +Л„).

Для вычисления Л (Р) по схеме Горнера требуется только v умножений и V сложений.

В качестве примера процедуры декодирования рассмотрим декодирование (15,5)-кода БЧХ, исправляющего три ошибки и имеющего порождающий многочлен

g (х) = х<> + х"" + )fi + + + X + I.

Для примера будем считать принятый многочлен равным v (х) = = л; + х. Ясно, что если бы произошло не более трех ошибок, то кодовое слово должно было бы быть нулевым и v (х) = е (х), но декодер не может сделать такого заключения. Выполним все шаги алгоритма декодирования. Сначала вычислим компоненты синдрома, используя арифметику в поле GF (16):

Si = + = а}\

Ss Se

= а" + а* = а\ = + а« = О, = + а* = а, = а? + а" = а«,

Пусть V = 3, тогда

Определитель M равен нулю; следовательно, полагаем v = 2. Тогда

Определитель не равен нулю; следовательно, произошло две ошибки. Далее,

м-1 =

О а"

следовательно,

Л (х) = aV + ах + 1.

7.3. КОДЫ РИДА -СОЛОМОНА 201

Используя процедуру Ченя, получаем разложение

Л (х) = (а-х + 1) (ах + 1) = а» (х - а) (х - а).

Многочлен локаторов ошибок Л (х) имеет корни а® и а, а локаторы ошибок равны элементам, обратным корням. Таким образом, ошибки произошли во второй и седьмой позициях. Поскольку код является двоичным, значения ошибок равны 1 и е (х) = = х + х.

7.3. КОДЫ РИДА-СОЛОМОНА

Важным и широко используемым подмножеством кодов БЧХ являются коды Рида-Соломона. Это такие коды БЧХ, у которых мультипликативный порядок алфавита символов кодового слова делится на длину кода. Таким образом, m = 1 и поле символов GF (q) совпадает с полем локаторов ошибок OF (q"). Обычно мы будем выбирать а примитивным; тогда

п = q - I = q -I.

Минимальный многочлен над GF (q) элемента 3, взятого из того же поля, равен

/р {х) = х- 3.

Поскольку поле символов и поле локаторов ошибок совпадают, все минимальные многочлены линейны. В коде Рида-Соломона, исправляющем t ошибок, обычно полагается /о = 1, и тогда порождающий многочлен записывается в виде

g (х) = (х ~ а) {х - а) ... (х - а-).

Степень этого многочлена всегда равна 2t, откуда следует, что параметры кода Рида-Соломона связаны соотношением

п -k = 2t.

В коде Рида-Соломона можно выбрать также любое другое значение /о, причем с помощью разумного выбора /о иногда удается упростить кодер. Таким образом,

g (х) = {х- а") (х ~ ai+) . . . (х - а/»+=-).

В качестве примера найдем g (х) для (15,П)-кода Рида- Соломона с t = 2 над (16). Может быть выбрано любое j; мы выберем /о = 1. Тогда

g (х) = (X - а) (х - а) (х - а) (х - а*) =

= X* -f (2 + 2 + 1) х + + z)x+zx + (z + z+l)==

= X* Н- aV + aV + ах + а"".

(Здесь использовано приведенное в табл. 7.1 представление элементов поля GF (16) в виде многочленов от г.) Поскольку сте-