1) При d s;C nl2. - Прим.

Теорема 14.4.3. Над GF [q) существуют коды со скоростью R и минимальным расстоянием d, для которых

Rl - (1/п) log, V, где V - объем сферы радиуса d.

Доказательство. Воспользуемся теоремой 14.4.2 и будем считать, что Г 1. Если это не так, то можно взять любую точку, у которой на расстоянии, не превышающем d, нет кодовых слов, и объявить ее кодовым словом, тем самым расширив код. Следовательно,

qk-ny 1

п - < log, V,

откуда следует утверждение теоремы.

Теорема 14.4.4 (граница Гилберта). Функция d (R) б для всех значений б, которые удовлетворяют неравенству

Rl-b log, {q-l)+6 log, б -f

+ (1-б) log, (1-6).

Доказательство. Объем V представляет сумму d слагаемых, из которых последнее является наибольшим ). Поэтому

V<diq-~irQ. Используя теорему 14.4.1 и сделав подстановку б = din, получим yd{q-\ - с - 6) log, (1 - 6) - о (1)]

где о (1) стремится к нулю при п, стремящемся к бесконечности. Далее,

-i- log, V < б log, (9 - 1) б log, б - (I - б) log, (1 - б) - о (1).

Подставив это неравенство в неравенство, доказанное в теореме 14.4.3 и опустив в асимптотике член о (1), завершим доказательство. □ Для двоичных кодов граница Гилберта принимает вид

R\-Hb id),

id) = -а iog2 J - (1 - d) logs (1 - d).

Графически эта граница изображена на рис. 14.7.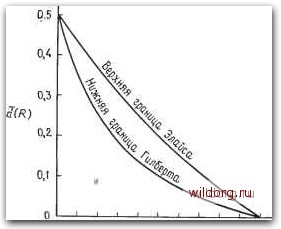

о 0,1 0,2 0,3 OA 0,5 0,6 0,7 0,8 0,9 1,0 Скорость /г

Рис. 14.7. Некотлрыг известные границы функции d (R) при <? = 2.

Теперь выведем верхнюю границу для d{R), называемую границей Элайса. Предположим, что код имеет М = е" кодовых слов длины п. Совместной композицией кодовых слов с и с называется таблица [п%] размера q X q, где элемент пи- определяет число позиций, в которых кодовое слово с содержит символ /, а кодовое слово с - символ /; следовательно,

d(c,c)=2 п%.

I. г

На расстоянии t от каждого кодового слова находится всего

слов; это число равно количеству слов, расположенных на сфере радиуса t.

Теорема 14.4.5. Пусть At - число кодовых слов на сфере радиуса t с центром в любой точке векторного пространства GF" (<?). Для заданного кода W мощности среднее число кодовых слов на сфере с центром в произвольной точке пространства равно

Доказательство. Так как на расстоянии t от кодового слова располагается At точек, оно лежит на At таких сферах. Поэтому сумма числа кодовых слов, расположенных на всех таких сферах, равна <?Л(, и среднее число кодовых слов на сфере равно <7Л(/<?". □

где dtot - общее расстояние, получаемое суммированием расстояний между неупорядоченными парами кодовых слов (не обязательно различных) на сфере:

с, с с, с I, I

Напомним, что [пи-] - это совместная композиция кодовых слов с и с. Упростим суммирование по с и с . Пусть пТг \i равно единице, если в t-й позиции с стоит /, а с имеет в этой позиции в противном случае оно равно нулю. Пусть Ti\i - число кодовых слов на сфере, имеющих / в /-Й позиции. Тогда

dioi = Л Ij Jj zz I / =

c, cZ.Z i

= 1j Yi Ij "zz- ic= Ti Ij Тц {Гi-\

i Z, Z с l+l-

Введем теперь величину

i I, I c, с i Z, I

l+l- l+l-

h\i = Тщ/Т,

равную доле кодовых слов на сфере, имеющих I в /-Й позиции Общее расстояние между такими кодовыми словами равно

tot = Т Л Ijll 11 I llli

I I, I

Выберем сферу так, чтобы на ней число кодовых слов было бы не меньше среднего. Удобно представить себе, что центром такой сферы является слово, целиком состоящее из нулей. Для этого достаточно так отобразить на себя исходное пространство, включая кодовые слова, чтобы центр выбранной сферы совпал со словом, целиком состоящим из нулей. Это не повлияет на минимальное расстояние кода.

Таким образом получим сферу радиуса t с центром в начале координат, на которой лежит Т кодовых слов, где Т не меньше q-"Af В дальнейшем величина t будет выбрана так, чтобы Т было достаточно большим и удовлетворяло нашим целям. Следующий шаг - оценка расстояния между двумя кодовыми словами, находящимися на сфере. Чтобы получить ее, оценим среднее расстояние между такими кодовыми словами

Т (Т - 1)