компонент на любой из оставшихся q - 2 ненулевых символов и любых / из оставшихся ненулевых компонент на нули. Ограничение / -Ь 1 + k = S гарантирует, что результирующее слово находится на расстоянии s от кодового слова. Ограничение / + -\- k - / = /1 гарантирует, что результирующее слово имеет вес h. □

Теорема 14.2.3. Если 2/ + 1 и декодер исправляет все

конфигурации ошибок, вес которых не превышает t, то вероятность ошибочного декодирования равна

Ре = I] [/(1 - Я)]" (1 - РГ" h t AiN{l, h; s).

/1=0 s=01=1

Доказательство. Число конфигураций ошибок веса h, которые приводят к ошибке декодирования, равно Ss=oZj"=i/ h; s); в силу условия 2/+ 1 <; d* ни одна из конфигураций ошибок не сосчитана дважды. Вероятность каждой из них равна [Р/{Я--Р)"~, что доказывает теорему. □

Теоремы 14.2.2, 14.2.3 и 14.1.2 содержат все необходимое для нахождения вероятности ошибки кода Рида-Соломона. Эта вероятность может быть вычислена непосредственно на ЭВМ. Приведенные соотношения легко модифицировать применительно к декодеру, исправляющему ошибки и стирания. Если число стираний равно р, то нужно просто заменить п на п - р, а Ре на условную вероятность ошибки Ре\р- Тогда если распределение вероятностей Q (р) числа стираний р известно, то Ре может быть вычислено по формуле Ре = TipPnpQ (р)-

14.3. РАСПРЕДЕЛЕНИЕ ВЕСОВ СВЕРТОЧНЫХ КОДОВ

Вес бесконечно длинного кодового слова сверточного кода равен числу его ненулевых компонент. Свободное расстояние - это вес кодового слова минимального веса. Свободная длина - это длина сегмента кодового слова минимального веса до его последнего ненулевого кадра включительно. Если код настолько прост, что его решетку можно построить непосредственно, то все эти параметры можно найти по решетке. Например, на рис. 14.4 перерисована решетка сверточного (6,3)-кода, исследованного в гл. 12. Один из путей имеет вес 5, и этот вес является минимальным расстоянием кода. Длина этого пути равна трем кадрам, поэтому свободная длина кода равна 6. Информационная последовательность пути, определяющего свободное расстояние, содержит одну единицу. Изучая далее решетку, увидим, что вес 6 имеют два пути, вес 8 - один путь и вес 10 - один путь. Таким образом

506 ГЛ. 14. композиция И ХАРАКТЕРИСТИКИ кодов

Бремя Состояние о 00 . 00

10 01

2. 3 4

00 00 . 00 . 00

00 00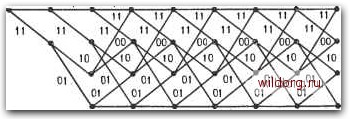

I 10 10 10 10 10 10

послеЭниО

nocmynueuiuD " бит

Рис. 14.4. Представление сверточного (6, 3)-кода с помощью решетки.

можно пересчитать число путей каждого веса, но это занятие быстро становится утомительным. В этом параграфе мы опишем более эффективную процедуру.

На рис. 14.5, а решетка после исключения временной оси сведена К диаграмме состояний. Для удобства эта диаграмма состояний перерисована на рис. 14.5, б с маркировкой путей. Так как мы интересуемся только путями, которые начинаются и заканчиваются 00, узел, маркированный символами 00, представлен дважды: один раз как вход, второй раз как выход. На этой диаграмме состояний легко проследить путь веса 5.

Вес пути можно найти проще, связав вклад каждого пути со степенью некоторой формальной переменной D и воспользовавшись методом, предложенным для анализа диаграмм состояний. Модифицированная диаграмма состояний приведена на рис. 14.6, где вес ребра представлен степенью D. Вес пути получается умножением вкладов всех ребер вдоль этого пути.

Вычислим общий вклад Т (D) совокупности всех путей между входом и выходом, решив следующую систему уравнений, найденных по рис. 14.6:

b = Dc +Db, c = Da + b, d = Dc + Dd, e = D%.

Решение этих уравнений дает

ре 1 - 2D

а,

Рис. 14.5. Диаграмма состояний для сверточного (6, 3)-кода. а

С = 00

6= 10 с = 01

6=11

е =00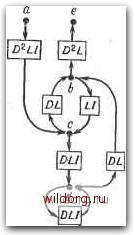

с =00 * = 10 с = 01 </=11 е = 00

Рис. 14.6. Модифицированная диаграмма состояний для сверточного (6, 3)-кода.

а - с перемзнной D, подсчитывающей задержку; б - с переменными D, L п f, подсчитывающими соответственно задержку, число кадров и число единиц на входе.

и поэтому передаточная функция равна

Т(В)= д = -L 2D + 4D f ... +2D"+5-f ....

Следовательно, вес k + 5 имеют 2 путей.

Тот же метод можно использовать для изучения других свойств кода. Введем две новые формальные переменные, а именно L для подсчета кадров и / для подсчета числа единиц на входе. Вклад любого ребра равен одному L; если ребро соответствует поступлению единичного входного символа, то его вклад равен