волы переданного кодового слова с равны нулю, и равны -] 1 в тех позициях, в которых символы с,, равны единице.

Пусть Сг - вектор в п-мерном евклидовом пространстве, такой, что его компоненты определяются выражением

I -1, если = О, "" ~ 1 +1, если ci = 1. Это выражение описывает отображение кодовых слов из GP (q) в Сохраним за с название кодового слова. Евклидово расстояние между принятым словом v и кодовым словом Сг равно

d (V, с,) = i V - Г" = Т (о-.

Если V состоит лишь из символов жесткого решения = ±1, то евклидово расстояние связано с хэмминговым расстоянием соотношением

dl (v, Cr) = 4Ля (v, с,),

где компоненты Vi вектора v равны О, если 0,- = -1, и равны 1, если t»j = 1. В частности, для любых двух кодовых слов

d {сг, Сг-) = 4Ля (Сг, Сг-У,

Минимальное евклидово расстояние кода и минимальное хэм-мингово расстояние d* связаны соотношением

d*E = 4dh.

Опишем О.МР-декодер с помощью скалярного произведения v-Cr, предварительно выразив евклидово расстояние кода через скалярное произведение. Мы можем переписать его в виде

dl{\, H.) = vP-2v.c.-f с.

Для фиксированного v минимизация (v, с.) по г эквивалентна максимизации скалярного произведения v-c по г, поскольку I V Р не зависит от г и с равно п для любого кодового слова. Минимизация евклидова расстояния интуитивно понятнее, но при вычислениях лучше максимизировать скалярное произведение.

Декодеру, исправляющему только ошибки, предшествует демодулятор, который принимает лишь жесткие решения. При этом и = ±1 и dl (V, Cr)=4dw(v, Cr). Следовательно, нахождение Сг на минимальном евклидовом расстоянии от v эквивалентно нахождению с на минимальном хэмминговом расстоянии от v. Неравенству

d« (V, с,) <: (d* - 1)/2

удовлетворяет не более одного кодового слова с. Следовательно, не более чем одно кодовое слово с удовлетворяет неравенству

dl (V, с,) < 2 (d* - 1).

Наконец, так как v Р равно п в случае демодулятора с жестким решением, то

d\.(y, Сг) = 2{n - v-Cr)

и не более чем одно кодовое слово удовлетворяет неравенству

V-C, п -(d*- 1),

где d* - минимальное хэммингово расстояние кода. Декодирование с исправлением только ошибок эквивалентно нахождению того единственного кодового слова с, для которого

V • Сг > п - d*,

если такое кодовое слово существует. Возможно, что решения не существует и декодер не в состоянии найти кодовое слово. Такой декодер неполон, но он будет указывать, что соответствующие конфигурации ошибок являются неисправляемыми.

Если действия демодулятора сводятся к жесткому решению или стиранию, то 0j = ±1 или 0. По тем же причинам, что и выше, декодирование с исправлением ошибок и стираний эквивалентно нахождению того единственного кодового слова с, для которого

v- > п - d*,

если такое кодовое слово существует. Как и ранее, соответствующий декодер полон.

Следующая теорема утверждает, что те же условия существования справедливы и при мягком решении.

Теорема 15.3.1. Каков бы ни был вектор v с компонентами, лежащими в интервале [-1, 1 ], в двоичном коде с длиной п и минимальным хэмминговым расстоянием d* существует не более одного кодового слова с, для которого

v-Cr > rt - d*.

Доказательство. Пусть с - некоторое кодовое слово, удовлетворяющее приведенному выше неравенству, и пусть с,--любое другое кодовое слово. Тогда с- отличается от Сг по меньшей мере Б d* позициях. Пусть

S = \i\cncri\;

тогда

v-Cr = 1] UjC,.i -j- Ti ViCi = Ai-\- Ла,

iS i€ s

V-C;-- = Y ViCr-i + 2j "iCr-i = A\ - A2. сфЗ i £ s

Ho величина удовлетворяет неравенству Л= Ij йДг < n - d*,

так как она равна сумме не более п - d* слагаемых, ни одно из которых не превышает единицу. Поэтому в силу неравенства V- Сг > п - d* Ла > О, и, следовательно, Л - А < п - d*, что завершает доказательство теоремы. □

В качестве примера рассмотрим двоичный (3,2)-код W = {ООО, ОН, ПО, 1011, у которого d* равно 2. Этот пример достаточно прост для графической иллюстрации теоремы 15.3.1. На рис. 15.4 изображен куб в трехмерном евклидовом пространстве, содержащий возможные принятые векторы v. В том же пространстве показаны четыре кодовых слова. Штриховкой в одном из углов выделена совокупность v, удовлетворяющая условию VgCro + + DjCri + УаСга > 1, Которая декодируется в кодовое слово, лежащее в этом углу. Теорема утверждает, что если построить аналогичные области для каждого из четырех кодовых слов, то эти области не будут пересекаться. Используя эти четыре области декодирования, можно построить ОМР-декодер. Заметим, что указанные четыре области не заполняют куб полностью. Остающаяся в центре область является тетраэдром, и если v

Койоеые слова

Койоеое слово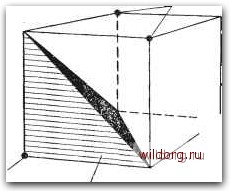

Койоеое слово

Область йекойирования

Рис. 15.4. Область декодирования по ОМР-алгоритму для двоичного (3, 2)-кода.