В.е. укорочённые циклические коды isl

etfea деления на g {х) путем выбора точки ввода v (х) в цепь деления. Покажем на примерах, как это делается.

Сначала приведем два примера декодероб для циклических кодов. Первым рассмотрим укороченный, циклический код, исправляющий пакеты ошибок. Предположим, что в некотором приложении потребовалось укоротить (511, 499)-код из табл. 5.1 до (272, 260)-кода. Этот код исправляет все пакеты ошибок длины не более 4. В данном случае g {х) = х -\- х -{- х + л; + 1,

251

И необходимо вычислить

а{х) = Rg(x) [хЧ

Одним из способов этого вычисления является представление

х в виде

с тем, чтобы воспользоваться равенством х = х -\- х х -\-\. Повторяя возведение в квадрат величины х и проводя редукцию по модулю g (х), быстро вычисляем (л;)* и (л: Y, а, следовательно, и к, так что

а (х) = -Ь + л; + -f х -I- 1,

Тактовый ееоЗ потока 272.-6umoebix Б/10к,ое с пакетом ошибок

Пппврпкп. нп. паврнство нилю I

После евоАа кажвых 272 Битов собержимое верхнего регистра перегружается в нижний регистр, а BepxHui регистр заполняется нулями

Проверка на равенство нулю восьми раэряЭов

272-Битовый буфер

Тактовый выеой потока исправленных 272-Битовых Блоков

Рис. 6.30, Декодер с вылавливанием ошибок для (272, 260)-кода, исправля-юш,его пакеты ошибок.

162 ГЛ. е. CkEMHAJt] РЕАЛИЗАЦИЙ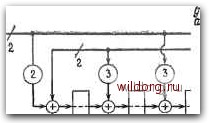

I Проверк.а на равенство нулю всех трех символов

Койовое слово

Рис,

Б4-разряВный регистр сВвига

Всего MS тактов ;. 6.31. Декодер Меггитта для (64, 60)-кода Хэмминга над GF (А).

И, наконец,

S {X) = [(" + + X- + X-\-X-+l)v (Х)].

Вычисление такого синдрома можно реализовать на одной цепи деления на g (х), если при каждой итерации входящий коэффициент многочлена v (х) подавать в соответствующую точку текущего остатка. Декодер Меггитта для рассматриваемого укороченного кода изображен на рис. 6.30. Этот декодер является конвейерным, так что он может обрабатывать непрерывный поток входящих битов.

В качестве второго примера рассмотрим (64 , 60)-код над GF (4), являющийся укорочением (85, 81)-кода Хэмминга. Как уже обсуждалось в § 5.5, (85, 81)-код Хэмминга является циклическим с порождающим многочленом g (х) = х -\- х -\-Зх -\- \. В данном случае х"-+ = х. Выполняя деление «уголком», получаем

а (х) i?;,4+;,3+3;,+, \х\ = х Зх + 2,

и модифицированный синдром задается равенством

S (л:) = Кх.+х+ъхм \{х + + 2) У (X)].

Показанное на рис. 6.31 устройство является декодером Меггитта для этого укороченного кода, время декодирования для которого равно 128 тактам. Для вычисления модифицированного синдрома

6.7. ДЕКОДЕР МЕГГИТТА ДЛЯ КОДА ГОЛЕЯ 183

декодер умножает принятое слово на + 2>х + 2 и затем делит на х +х +2>х -\- 1. Полное время декодирования, равное 128 тактам, состоит из 64 тактов, необходимых для вычисления модифицированного синдрома, и 64 тактов, необходимых для исправления ошибок. При желании можно сделать декодер конвейерным или последовательно соединить два декодера так, чтобы декодер работал одновременно с вводом данных.

6.7. ДЕКОДЕР МЕГГИТТА ДЛЯ КОДА ГОЛЕЯ

В тех случаях, когда данный код не позволяет непосредственно использовать декодер с вылавливанием ошибок, иногда удается так добавить несколько дополнительных цепей, чтобы аннулировать влияние некоторых мешающих применению декодера конфигураций ошибок. В общем случае для получения удовлетворительного решения требуется некоторая изобретательность. Мы опишем такой декодер для (23, 12)-кода Голея.

Длина вектора ошибок равна 23, а вес не превосходит 3. Длина синдромного регистра равна И. Если данная конфигурация ошибок не вылавливается, то она не может быть циклически сдвинута так, чтобы все три ошибки появились в 11 младших разрядах. Можно убедиться (возможно, после нескольких прикидок), что в этом случае по одну сторону от одной из трех ошибочных позиций стоит по меньшей мере пять, а по другую сторону - по меньшей мере шесть нулей. Следовательно, каждая исправляемая конфигурация ошибок может быть с помощью циклических сдви < гов приведена к одному из трех следующих видов (позиции нумеруются числами от О до 22):

1) все ошибки (не более трех) расположены в И старших разрядах;

2) одна ошибка занимает пятую позицию, а остальные расположены в 11 старших разрядах;

3) одна ошибка занимает шестую позицию, а остальные расположены в 11 старших разрядах.

Таким образом, в декодере надо заранее вычислить величины S5 {х) = Rgx) и S6 {х) = Rgix) [л:"-*л*]. Тогда ошибка

вылавливается, если вес s (х) не превышает 3 или если вес S (х) - Sg (х) либо S (х) - Se (х) не превышает 2. В декодере можно либо исправлять все три ошибки, если эти условия выполнены, либо исправлять только две ошибки в младших 11 битах, дожидаясь удаления из регистра третьего ошибочного бита. Разделив и л: на порождающий многочлен

g (х) = + + х« + + X* + + 1,