Доказательство сводится к комбинации трех простых утверждений.

(i) По определению

v{x)=g (х) Qi (X) + S (х), XV [х) = xg (x)Qi (х) + XS (х),

(ii) XV (х) (mod х" - 1) = ху (х) - (х" - 1) у„ ]..

(iii) Согласно алгоритму деления,

XS {х) = g (х) (х) + t (х)

однозначно, причем deg t (х) < deg g (х). Комбиниря эти утверждения, получаем

XV (X) (mod х« - 1) = [xQi (X) + (х) + vJi {х) ]g{x)t (х) =

= ix) g{x) + t (x).

Так как deg t (x) < deg g (x), то, согласно алгоритму деления, t (х) определяется однозначно и

t (х)*= /?g [XV (х) (mod х« - 1)] = [xs (х)],

что и требовалось доказать. □

Из этой теоремы, в частности, следует, что многочлены ошибок и соответствующие им синдромные многочлены удовлетворяют равенству

Rg ix) [хе (х) (mod X" - 1)] = Rg м [xs (х)].

Если е (х) - исправляемая конфигурация ошибок, то многочлен

е (х) = хе (х) (mod х" - 1)

получается циклическим сдвигом многочлена е (х). Следовательно, е (х) также является исправляемой конфигурацией ошибки, и его синдром дается равенством

S (х) = Rg [е (х) ] = Rg м Ixs (х) ].

Это соотношение показывает, как вычислять синдром произвольного циклического сдвига конфигурации ошибки, синдром которой известен. Такое вычисление можно реализовать на простой цепи с регистром сдвига, что, как правило, намного проще, чем просмотр таблицы синдромов.

Предположим, что s (х) и (х) представляют собой вычисленные синдром и ошибку соответственно и что надо проверить, является ли s (х) синдромом для многочлена ошибок ё (х). Проверим, выполняется ли равенство s (х) = s (х); если да, то мы знаем, что е (х) = ё (х). Если нет, то вычислим Rg [xs (х) ] и сравним его с s (х). Если они совпадают, то

ё(х) = хе (х) (mod х" - 1)

Принятое слово

Обратная связь цепи Веления на дсх)

<+)-* гл-Л-разряВный регистр сВвиго

Проверка на совпайение со всеми табличными синйромами

Буфер

7-разряВный регистр сйвига

Рис. 6.18. Декодер Меггитта,

Представляет собой циклический сдвиг многочлена е (х), так что мы знаем е (х). Продолжая таким образом, вычислим Rg ix) [xRg (л;) [xs (х) ] ]; в случае совпадения этого многочлена с s{x), заключаем, что ё (х) равен хе (х) (modx" -1), и т. д.

Составим таблицы из таких конфигураций ошибок, чтобы каждая исправляемая конфигурация была циклическим сдвигом одной (или нескольких) из них. Тогда в декодере необходимо запомнить только эту таблицу и таблицу соответствующих синдромных многочленов. Истинный синдром s (х) сравнивается со всеми синдромами, которые содержатся в таблице. Затем вычисляется Rg ix)[xs (х)] и тоже сравнивается со всеми содержащимися в таблице синдромами. Повторая этот процесс п раз, находим любую исправляемую кодом ошибку.

Обычно при использовании в декодере цепей с регистром сдвига в качестве табличных конфигураций ошибок выбираются такие, у которых ненулевые коэффициенты расположены в конце регистра сдвига. Это позволяет уменьшить число проводов и использовать регистры, начальные разряды которых не имеют прямого доступа. Такая реализация показана на рис. 6.18.

В качестве табличных выбираются все синдромы, соответствующие исправляемым ошибкам с ненулевыми старшими компонентами. В начале работы декодера содержимое всех разрядов регистра равно нулю. Сначала в декодере срабатывает цепь деления на g (х). В результате такой операции в регистре цепи деления записан синдром s (х), а буферный регистр содержит принятое слово. Вычисленный синдром сравнивается со всеми табличными синдромами, и в случае совпадения хранящийся в старшем разряде буфера символ исправляется. После этого синдромный регистр и буферный регистр один раз циклически сдвигаются. Это

реализует умножение синдрома на х и деление результата на g (х). Содержимое разрядов синдромного регистра теперь равно многочлену Rgix) [xs (х)], представляющему собой синдром ошибки хе (х) (mod х" - 1). Если этот новый синдром совпадает с одним из табличных синдромов, то в предыдущей по старшинству позиции произошла ошибка, которая теперь появится в последнем разряде буфера. Этот бит исправляется, и производится новый циклический сдвиг на одну позицию; синдромный регистр опять готов к проверке ошибки в позиции, отстоящей от старшей на два такта. После повторения этого процесса п раз все биты будут исправлены.

Показанная на рис. 6.18 обратная связь, предназначенная для исправления записанных в буфере символов, не является необходимой; вычисленные символы можно передавать непосредственно пользователю. Мы показали эту связь на схеме для того, чтобы проиллюстрировать идею о том, что только после последнего сдвига в буфере будет записано правильное кодовое слово, а также для того, чтобы иметь отправную точку для некоторых реализаций декодера, которые будут описаны ниже.

Приложения теоремы Меггитта лучше всего пояснить на конкретных примерах. Рассмотрим (15, 11)-код Хэмминга, задаваемый порождающим многочленом g (х) = х* + х + 1. Так как этот код исправляет только одну ошибку, то имеется только одна конфигурация ошибки с единицей в старшем разряде, а именно е (х) = х*, и соответствующий ей синдром равен s (х) = х + 1. Декодер Меггитта для этого кода изображен на рис. 6.19. Вычисленный по принятому слову синдром будет содержаться в синдром-ном регистре после 15 сдвигов. Из них первые 4 сдвига нужны только для того, чтобы ввести в регистр данные, без которых нельзя начать деление. Если синдром равен (1001), то е (х) = х* и соответствующий бит исправляется. Если после одного сдвига синдром равен (1001), то е (х) = х и соответствующий бит исправляется. Таким же способом проверяется необходимость исправления каждого из битов. После 15 таких сдвигов процесс исправ-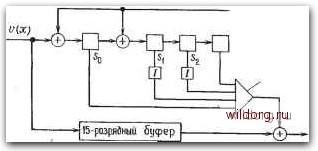

Проберка h равенства

s{x) =х +1

с(х)

Рис. 6.19. Декодер Меггитта для (15, 11)-кода Хэмминга.