,.(х) = х" + х х + .хV х« + х + х\+ 1 е(х) = х" +х

i;(x) = x* + .x"+.x- + x"+.4-° + .x* + x. + x* + x+l 11001001ibiiiII

Tr,,,m СинйромныО -г„„„ СреЭний -г Нижний регистр аш pjp Такт рр

Рис. 6.26. Пример вылавливания ошибок для (15, 7)-кода БЧХ.

будет показано, что этот код исправляет две ошибки. Сейчас мы примем это утверждение без доказательства.

Исправляемые конфигурации ошибок содержат не более двух ненулевых символов и задаются многочленом степени не выше 6. Их всегда можно циклически сдвинуть в многочлен степени не выше 3. Так как степень синдромного многочлена не превосходит 3, то можно применить декодирование с вылавливанием ошибок.

Такой декодер показан на рис. 6.27. В двоичной реализации восьмеричные разряды регистра сдвига представляют собой параллельные регистры с тремя двоичными разрядами. Все линии не-

Bxofl (7 восьмеричных

символов) 3 -i-

Цепь Веления на д{.х)=х!с№х ах+а?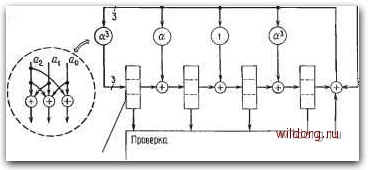

восьмеричный разряэ

на наличие ломеньшей мере йвух нулевых foumoB

(ВьЕорка трех инфор-Дмационных байтов)

Всего 21 такт

Рис. 6.27. Вылавливание ошибок для (7, 3)-кода Рида-Соломона.

редачи данных в каждый момент времени передают три бита. Элементы умножения на z + 1 (т. е. на а) и на z (т. е. на а) в цепи обратной связи являются просто определяемыми устройствами двоичной логики с тремя входами и тремя выходами. Для исправления всех ошибок такому декодеру необходим всего 21 такт. Первые семь тактов уходят на вычисление синдрома; следующие семь тактов требуются на исправление хотя бы одной ошибки, а иногда и обеих ошибок. Последние семь тактов уходят на исправление второй ошибки (если она еще не исправлена).

На рис. 6.28 отдельные операции алгоритма декодирования отслеживаются в деталях. Это очень ценный пример, так как он демонстрируе? технику вылавливания ошибок и одновременно представляет собой конкретный пример взаимосвязи абстрактных понятий теории полей Галуа и практического построения логических цепей, использующих регистры сдвига.

Содержимое синдромного и информационного регистров для каждого сдвига выписаны в таблице. После семи сдвигов синдромный регистр содержит синдром. Начиная с восьмого сдвига декодер исправляет ошибки, если они образуют вылавливаемую кон-

Рис. 6.28. Пример вылавливания ошибок.

фигурацию. К ним принадлежат ошибки, содержащие не более двух ненулевых символов, один из которых расположен в крайней правой позиции. Если произошло не более двух ошибок, то это случится хотя бы однажды в течение следующих семи тактов работы (в примере это случилось на 13-м такте). Следовательно, ошибка выловлена. Подчеркнем, что символы синдрома упорядочены в порядке возрастания слева направо. В момент вылавливания ошибки в синдромном регистре записан 4-символьный сегмент {е, 65, е, бо) сдвинутого многочлена ошибки. Поскольку