пень g (х) равна 4, п - й = 4ий=11. Информационный многочлен представляет собой последовательность одиннадцати символов из Gf (16), что эквивалентно 44 битам.

В качестве второго примера найдем g {х) для (7, 3)-кода Рида- Соломона с t = 2 над GF (8). Может быть выбрано любое /(,; мы выберем /о = 4. Тогда

g (х) = (х - а*) (х - а) (х - а") (х - а») =

= X* + (z + 1) х« + (z + 1) х + (г + 1) X + Z

(здесь использовано представление элементов поля GF (8) в виде многочленов от z). Информационный многочлен представляет собой последовательность трех восьмеричных символов (что эквивалентно девяти битам). Предположим, что

i (х) = (Z + Z) х2 + X + (Z + 1).

Кодовое слово несистематического кода запишется в виде

с (х) = i (х) g (х) =

= (а*х2 + X + а) (х« + aV + aV + Л + а) =

= ах" + ах5 + + Ох« + Ох + етх + а*,

что представляет собой последовательность семи восьмеричных символов.

Коды Рида-Соломона являются оптимальными в смысле границы Синглтона.

Теорема 7.3.1. Код Рида-Соломона имеет минимальное расстояние п - k + \ и является кодом с максимальным расстоянием.

Доказательство. Пусть d = 2 + 1 - конструктивное расстояние кода. Минимальное расстояние d* удовлетворяет неравенству

d* d = 2t + \ = п - k + \,

поскольку для кодов Рида-Соломона 2t = п - k. Но для любого линейного кода имеет место граница Синглтона

d* < n - k+l.

Следовательно, d* = п - k I и d* = d. П

Доказанная теорема утверждает, что при фиксированных п и й не существует кода, у которого минимальное расстояние больше, чем у кода Рида-Соломона. Этот факт часто является веским основанием для использования кода Рида-Соломона. Не стоит, однако, понимать это утверждение буквально. Часто предпочтение отдается кодам с такими параметрами (п, k).

при которых не существует кода Рида-Соломона. В то же время коды Рида-Соломона всегда оказываются короче всех других циклических кодов над тем же алфавитом.

7.4. СИНТЕЗ АВТОРЕГРЕССИОННЫХ ФИЛЬТРОВ

При использовании описанного в § 7.2 алгоритма декодирования кодов БЧХ основной объем вычислений приходится на решение системы уравнений

... 5,

• • • Sv+l

с Щ - • -v+i-

Si 5, Si 5з Ss S

s, s.

... S:

2V 1

При небольших значениях v эту систему можно решить с помощью обращения матрицы. Для обращения матрицы размера v X v необходимо произвести порядка действий. Однако на практике часто требуется использовать коды, исправляющие большое число ошибок, и в таких случаях желателен более эффективный метод решения данной системы. Такой метод был разработан Берлекэмпом. В основе этого метода лежит тот факт, что выписанное выше матричное уравнение не произвольно: матрица обладает специальной структурой. Это позволяет существенно упростить связанные с нахождением вектора А вычисления, хотя сама процедура вычислений становится более сложной для понимания, чем простое обращение матрицы.

Остановимся на предложенном Месси варианте алгоритма, который понял, что наилучший способ реализации алгоритма состоит в переформулировке задачи в виде задачи построения схемы с использованием регистров сдвига с линейной обратной связью. Предположим, что нам известен вектор А. Тогда первая строка выписанной выше системы [определяет значение через значения Sj, S, вторая строка определяет S+g через 2. S+i и т. д. Этот последовательный процесс описывается уравнением

S} = - iAiSj t, / = V + 1,.. -, 2v.

Для фиксированного А это уравнение определяет авторегрессионный фильтр. Он может быть реализован как регистр, сдвига с линейной обратной связью, множители в отводах которого задаются вектором А.

Переформулированная таким образом задача сводится к построению изображенного на рис. 7.2 регистра сдвига с линейной обратной связью, генерирующего известную последовательность компонент синдрома. Задача состоит в том, чтобы среди большого числа таких регистров найти регистр сдвига с наименьшей длиной. Это позволит определить вектор ошибок минимального веса в принятом слове, или, что то же самое, определить многочлен Л наименьшей степени. Многочлен минимальной степени имеет степень v и определяется единственным образом, поскольку матрица размера v X v исходной системы уравнений обратима.

Процедура построения авторегрессионного фильтра является также методом решения матричного уравнения относительно вектора Л. Ний<е будет приведена процедура построения такого регистра сдвига. Описанный метод окажется применимым для вычисления в любых полях и не будет предполагать каких-либо особых свойств последовательности Sy, S, Saf. Эта последовательность не обязательно должна состоять из компонент синдрома, но если ее элементы все же являются компонентами синдрома для исправляемой конфигурации ошибок, то процедура всегда приведет к регистру сдвига с ненулевым весовым множителем в самом правом отводе. Для произвольного регистра сдвига с линейной обратной связью, описываемой многочленом Л (х), длина регистра может быть больше, чем степень Л (х), поскольку несколько самых правых ячеек регистра может быть не охвачено обратной связью.

Для построения требуемого регистра сдвига необходимо найти две величины: длину регистра сдвига L и многочлен обратной связи Л (х):

Л (х) = Л.х + Л 1Х-1 + ... + AjX + 1,

где deg А (х) < L. Обозначим эту пару через (L, Л (х)). Необходимо найти регистр сдвига с обратной связью наименьшей длины, который генерирует последовательность Si, Sit, при соответствующем начальном состоянии.

Процедура построения регистра является индуктивной. Для каждого г, начиная с г = 1, построим регистр сдвига, генериру-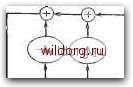

----Sj,.?,!

В начальном состоянии сойержит послеВовательность Sp, ,..., .S,

Рис. 7.2. Многочлен локаторов ошибок в цепи регистра сдвига.