9.5. ДЕКОДИРОВАНИЕ ВО ВРЕМЕННОЙ ОБЛАСТИ 307

ваться преобразованием Фурье, а нужна некоторая перестройка.

Теорема 9.5.2. Пусть v = с -f е - - принятое заилумленное слово кода БЧХ. При заданном во временной области векторе локаторов ошибок Х решением множества рекуррентных уравнений

является wl" = е,-, i О, п - 1.

Доказательство. Разобьем шаг рекурсии в частотной области на два шага, начиная с принятого спектра V и покомпонентно преобразуя его в Е:

/ п-1 \ /г-1

\ /=1 / /=о

Так как yf" = Ef для / = 1, 2 и Л; = О для / > t, то выписанные выше уравнения эквивалентны следующим:

Эта эквивалентность и доказывает теорему. □

На рис. 9.7 изображен временной декодер для полейхарактеристики 2. Левая часть блок-схемы соответствует теореме 9.5.1, а правая - теореме 9.5.2. В процессе проведения итераций в левой части формируется преобразование Фурье многочлена локаторов ошибок. При каждой итерации в правой части принятое слово преобразуется таким образом, что одна компонента спектра принятого слова переходит в компоненту спектра вектора ошибок. Таким образом, после выполнения последней итерации принятое слово преобразуется в вектор ошибок.

Привлекательность декодера во временной области объясняется двумя причинами.

1. Вычисления проводятся в один этап, а процедура Ченя и рроцедура вычисления синдрома отсутствуют. Это приводит п более экономной конструкции, особенно при аппаратурной кеализации отдельных блоков декодера.

2. Такой декодер при умеренных значениях п должен выполнять намного меньше вычислений, чем декодер, использую-

Начальные значения:

Si =Ui

>i = 6i = l, i = 0,...,n-l Z.=r=0

г-г+1

Вычисление слейуюш,его выхойа послейнего фильтра

Вычисление лонатора

Вычисление преобразования нового многочлена связей, йля которого Лг=0

:=0,...,п-1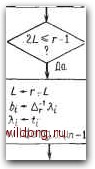

5;-Si-Ага

г = 0,...,п-1

Cmon-исправление закончено

1=0.....п-1

Рис. 9.7. Временной декодер.

щий Прямое преобразование Фурье и общепринятый алгоритм Б ер л екэмп а-Месси.

Независимо от числа исправляемых ошибок работа декодера занимает п тактов. Так как за каждый такт обрабатывается вектор размерности п, то сложность декодера является величиной

О (п)- При больших п МОЖНО построить декодер с меньшим числом вычислений. Однако для малых п, включающих интервал практически используемых длин кода, временной декодер более привлекателен и обладает простой структурой. В эпоху больших интегральных схем структурная простота по меньшей мере столь же важна, сколь и число арифметических операций.

9.6. ДЕКОДИРОВАНИЕ ЗА ГРАНИЦЕЙ БЧХ

Часто случается, что конфигурации ошибок, вес которых мало отличается от радиуса упаковки кода, не попадают ни в одну сферу декодирования. Такие лежащие между сферами декодирования ошибки не совсем обоснованно называют неисправляемыми конфигурациями ошибок. Они обычно обнаруживаются, но не исправляются. Иногда удается исправить некоторые из этих ошибок, расширив множество исправляемых конфигураций ошибок. Укажем некоторые методы, позволяющие выполнить такое декодирование.

Распознать неисправляемые кодом БЧХ конфигурации ошибок можно либо по тому, что число корней многочлена локаторов ошибок, лежащих в поле локаторов, не равно его степени, либо по тому, что компоненты вектора ошибок выходят за пределы поля символов GF {q). Чтобы обнаружить такие ситуации, нет необходимости полностью выполнять все вычисления алгоритма декодирования: они могут быть распознаны по свойствам рекуррентно вычисляемого спектра ошибок:

Е] = - S Aftfjjj.

Согласно теореме 8.2.1, принадлежность всех компонентов конфигурации ошибок полю GF (q) можно распознать, проверив выполнение условия Е) ="((/9)) для всех индексов / в спектре этой конфигурации. Если такая проверка указывает на неисправ-ляемую конфигурацию, то вычисления прерываются. Требование, состоящее в том, что степень многочлена Л {х) равна числу корней многочлена Л (х) в поле GF {(f"), можно проверить с помощью условия периодичности последовательности коэффициентов {Ej\ : Еп+п) - Ej для всех /. Таким образом получается второе правило проверки для обнаружения неисправляемой конфигурации ошибок и прекращения декодирования. Это правило основывается на следующей теореме.

Теорема 9.6.1. Предположим, что А{х) является ненулевым многочленом наижньшей степени, удовлетворяющим условию

deg л (/г) £/ = - Ij AkEj k