ошибка поймана, она исправляется в информационном регистре, а в синдромном регистре во устанавливается равным нулю (или вычитается сам из себя). После 14 тактов синдромный регистр содержит синдром оставшейся конфигурации ошибки. Процесс повторяется в течение последних семи тактов, после чего исправление ошибок закончено полностью.

Если в начале синдром оказался отличным от нуля, а в течение вторых семи тактов работы декодера не была поймана ни одна ошибка, то в принятом слове произошло более двух ошибок (но обратное утверждение неверно). Это позволяет легко включить в декодер дополнительную логическую цепь для обнаружения неисправляемых конфигураций ошибок.

В качестве "последнего примера этого параграфа рассмотрим декодер с вылавливанием ошибок для кодов, исправляющих пакеты ошибок. В отличие от ситуации для кодов, исправляющих независимые ошибки, исправляющие пакеты ошибок коды всегда допускают декодирование с вылавливанием ошибок. Мы опишем декодер для (14, 6)-кода, исправляющего пакеты ошибок длины 4. Этот код получается перемежением двух копий (7, 3)-кода из табл. 5.1. Порождающий многочлен кода-перемежения равен

g (х) = + + + \ .

Вылавливание пакета ошибок длины не более 4 сводится к проверке равенства нулю четырех самых левых символов синдрома. Схему, однако, можно немного улучшить. Заметим, что разряды с четными номерами и разряды с нечетными номерами не взаимодействуют. Поэтому цепь вычисления синдрома можно рассматривать как две независимые цепи вычисления синдромов для каж-

Ввой Iff Битов, собержйщих пакет ошибок.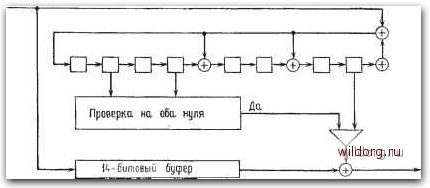

Всего 1Ъ тактов

Вывов М ffumoB Без оши&ки

Рис. 6.29. Декодер с вылавливанием ошибок для кода-перемежения, исправляющего пчкеть! ошибок,

6.6. Vkot>04EHHbiE циклические Кбды if§

ДОо из двух перемежаемых кодов, но с последующим перемеже нием позиций синдромов. Такая модификация декодера с вылавли ванием ошибок показана на рис. 6.29. Этот декодер позволяет ис» правлять все пакеты ошибок длины 4, а также некоторые дополнительные конфигурации ошибок. Исправляется любая конфигурация, состоящая из пакета Длины 2 в позициях с нечетными йомерами и пакета длины 2 в позициях с четными номерами,

6.6. УКОРОЧЕННЫЕ ЦИКЛИЧЕСКИЕ КОДЫ

Любой систематический циклический код можно укоротить, а именно от (п, к)-кода можно перейти к (п - Ь, k - &)-коду выбрасыванием Ъ информационных позиций в каждом кодовом слове. Будем полагать, что b меньше k и что выбрасываются b старших разрядов. Последнее объясняется тем, что выбрасываемые символы при укорочении полагаются равными нулю и поэтому не передаются, но при декодировании декодер их восстанавливает, так что декодирование осуществляется на полней длине кода. Если минимальное расстояние исходного кода равно d*, то минимальное расстояние укороченного кода не меньше d*. Аналогично если исходный код позволяет исправлять пакеты ошибок длины t, то укороченный код позволяет исправлять пакеты длины t (или больше). С помощью укорочения и перемежения из кодов табл. 5.1 можно построить большой набор хороших кодов, исправляющих пакеты ошибок.

Укороченный циклический код уже не является циклическим, так как многочлен Rn i ixc (х)] в общем случае уже не является кодовым словом для произвольного кодового слова с (х). Однако укороченный циклический код все-таки обладает алгебраической структурой подмножества соответствующего кольца. В то время как циклический код является идеалом кольца многочленов по модулю X" - 1, укороченный циклический код является идеалом кольца многочленов по модулю некоторого многочлена / (х) степени п = п - Ь. Точный результат дается следующей теоремой.

Теорема 6.6.1. Еслиё -укороченный циклический код, то существует многочлен f (х), такой, что если с (х) - кодовое слово, а а (х) - произвольный многочлен, то Rf х) f« (х) с (х) ] также является кодовым словом.

Доказательство. Пусть g (х) - порождающий многочлен укорачиваемого циклического кода длины п, и пусть п - длина укороченного циклического кода. Тогда, согласно алгоритму деления,

X" =g{x)Qix) +8{Х).

Так как п = п -Ь>п - k = deg g (х), то степень остатка s{x) меньше п. Пусть f (х) = х"- - six); тогда степень много-

180 гл. 6. схЕлшАя реализации!

члена f (х) равна п и g (х) делит f (х). Если с (х) кратен g (х) и а (х) - произвольный многочлен, то, согласно алгоритму деления, имеем

а (х) c{x) = t {X) Q {х) + г {х).

Так как g {х) делит и с [х), и / {х), то г {х) кратен g {х); таким образом, в кольце GF{q)[xV{f (х)) многочлен а (х) с [х) = г {х) кратен многочлену g{x), что и требовалось доказать. □

Укороченный циклический код длины п = п - Ъ можно декодировать с помощью декодера Меггитта, сконструированного для исходного (п, )-кода. Отсчет времени в таком декодере основан на rpynnaji: по п тактов, хотя входное кодовое слово содержит п символов. Это временное рассогласование иногда удается устранить конструкцией устройства, так что оно становится несущественным; в других случаях целесообразнее сбалансировать время. Мы рассмотрим такую модификацию принятого слова, которая позволяет перестроить работу декодера Меггитта на цикл из п тактов и соответственло ускорить декодирование укороченных циклических кодов.

Переопределим синдром так, чтобы можно было обойти тактовое время работы регистра, соответствующее выбрасываемым символам. Вместо вычисления остатка от деления многочлена X"-- V (х) на g (х) определим синдром при Ъ выбрасываемых символах равенством

s{x\Rgx)[x-~+v{x)\.

Чтобы обосновать такой выбор, предположим, что старший символ укороченного циклического кода ошибочен, т. е. что

e(x) = e„ ix"-)-.

Тогда

s(x)=-./?g [е„- ,х2"-"-Ч =

= Rg W [Rxn , [e„, ix2"-*-]] = e„. iX"-"-i.

Следовательно, единственным ненулевым коэффициентом многочлена S (х) является старший коэффициент. Пусть

Тогда, согласно правилам вычислений по модулю, многочлен S (х) можно записать в виде

S (х) = Rgx [а (х) v (х)].

Все, что нужно сделать, сводится к предварительному (перед делением на g (х)) умножению v (х) на фиксированный многочлен а (х). Такое умножение можно реализовать с помощью устрой-