I 9.3. РАСШИРЕННЫЕ коды РИДА-СОЛОМОНА 301

из 2 i компонент синдрома начинается с компоненты S, равной 1 „, и заканчивается компонентой S-2t, равной Vf+2t-i - v. Предположим, что произошло не более t ошибок, и проведем итерации алгоритма Берлекэмпа-А1есси от до Su-i- Если L2t 2 < <: - 1 и невязка Agjj равна нулю, то, согласно теореме 7.5.3, во внутреннем векторе произошло не более t- 1 ошибок и вычисленное значение многочлена локаторов ошибок правильно. В противном случае во внутреннем векторе произошло t ошибок, и, следовательно, символ правилен. Дополнительная компонента синдрома Sat позволяет продолжить алгоритм Берлекэмпа- Месси еще на один шаг, так что полное число итераций равно 2t, и поэтому найден многочлен локаторов t ошибок. Декодер для расширенного на одну позицию кода Рида-Соломона показан на рис. 9.5.

Декодер для расширенного на два символа кода Рида-Соломона более сложен и описать его труднее. Предположим, что произошло не более t ошибок. В нашем распоряжении имеются 2t- 2 компонент внутреннего синдрома, начиная с компоненты Si, равной Vj+i. Согласно теореме 7.5.3, воспользуемся ими для исправления 2t-2 ошибок во внутреннем векторе и обнаружения i ошибок. Иначе говоря, начиная с S и выполняя 2t-4 итераций алгоритма Берлекэмпа-Месси, найдем многочлен локаторов ошибок. Если /.24 4 < t- 2, то сделаем еще две итерации и остановимся, если хотя бы одна из невязок A2t 3 или A2t-2 отлична от нуля. Если обе невязки равны нулю, то во внутреннем векторе произошло не более 2t-2 ошибок. В этом случае многочлен локаторов ошибок вычислен правильно и может быть использован для дальнейшего исправления ошибок во внутреннем векторе. Так как полезная информация может быть полностью выделена из внутреннего вектора, то декодирование закончено. В противном случае внутренний вектор содержит f- 1 или t ошибок, и поэтому искажено не более одного граничного символа. Следовательно, хотя бы одна из компонент So и

-24-1 синдрома правильна, а если все ошибки произошли во внутреннем векторе, то они правильны обе. Присоединяя сначала одну, а затем вторую из них к остальным компонентам сшщрома, получим два блока по 2t- 1 символов, хотя бы один из которых содержит 2t- 1 правильных компонент синдрома.

Теперь дважды применим алгоритм Берлекэмпа-Месси, сначала к одному из этих блоков (от So до а затем к другому (от Si до Sat.i). Каждый раз будем исправлять t- I и обнаруживать t ошибок. Если все ошибок расположены во внутреннем векторе, то обе попытки позволят обнаружить t ошибок во внутреннем векторе, и, следовательно, оба символа расширения являются правильными. Если при одной или при обеих попытках не обнаруживается t ошибок, то во внутреннем векторе произошло

Начальные значения:

л№) =bfjc) = 1 L = r=0. e = l

Hera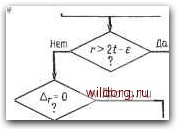

Да-вычисление граничной компоненты синйрома Вля

слейугащего

шага

Г(д:)-Л(х)-А;.х£Сх)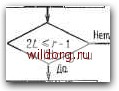

Л(х)-7№)

Lr-L A(x}-r(j:)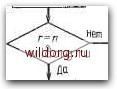

;• =0,...,п-1

Cmon-исправление закончено

Рис. 9.5. Декодер для расширенного на один символ кода Рида-Соломона.

только t- 1 ошибок, и, следовательно, многочлен локаторов ошибок вычислен правильно и может быть использован для исправления внутреннего вектора. Так как информация может бьггь полностью извлечена из внутреннего вектора, декодирование закончено.

Наконец, если во внутреннем векторе обнаружено t ошибок, то оба граничных символа правильны. Следовательно, и обе граничные компоненты синдрома также правильны, и в нашем распоряжении имеется 2t правильных компонент синдрома, позволяющих исправить / ошибок во внутреннем векторе.

Описанная процедура декодирования все же дважды обращается к алгоритму Берлекэмпа -Месси. Такое описание выбрано из соображений простоты объяснения; процедуру можно сделать более компактной.

9.4. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ БЧХ

Теперь мы можем описать декодирование расширенных на два символа кодов БЧХ, определенных в § 8.5. Если конструктивное расстояние d кода является нечетным числом, то представленный в расширении поля код со своими хвостами образует подкод кода Рида-Соломона, и можно использовать уже описанный декодер для расширенного на две позиции кода Рида-Соломона. Если конструктивное расстояние кода четно, то к одному из хвостов добавим проверку на четность. Пока еще без доказательства мы утверждаем, что эта процедура приводит к коду, минимальное расстояние которого не меньше d \. Докажем этот факт, выписав соответствующий алгоритм декодирования. Декодер аналогичен декодеру для расширенного на два символа кода Рида-Соломона.

Теорема 9.4.1. Расширение на два символа двоичного кода БЧХ с четным конструктивным расстоянием d при использовании дополнительной проверки на четность на одном из хвостов приводит к коду, минимальное расстояние которого равно по меньшей мере dj-f 1.

Доказательство. Пусть t=d/2. Построим декодер, исправляющий ошибок. В нашем распоряжении имеются 2t-3 компонент внутреннего синдрома и две граничные компоненты синдрома So = V/„ - и Sts = V;„ 2/-2 - v+, которые правильны, если граничные символы v и не содержат ошибки. По предположению конструктивное расстояние d является четным числом, а в силу ограничений сопряженности числа /о и jo+t-2 должны быть нечетными. Эти требования выполняются только в том случае, когда /о < О и /о -f 2 i - 2 > 0. Следовательно, ограничения сопряженности гарантируют также, что Су-i = О и С;„+2; , = О, так как частоты (/о - 1)/2 и (/o+2i-1)/2 являются четными. Следовательно, мы имеем еще две компоненты синдрома, а именно .S i= V/„-i и St-i = Vj+zf-i-

Так как дополнительно содержит проверку па четность, ТО можно определить, четно или нечетно число произошедших