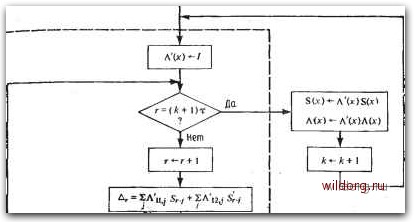
i<-6(r-i) + (l-6)i

1 -ЛЛ

6 (1 -6): Д„--5Д,+ (1-6)Д,„

Алгоритм Берлекэмпо.- Месси

Л(г)-А(х)А(д:) A(jr)->-Ail(*) + A2(x)

Стол

Рис. М.7 Ускоренный алгоритм Берлекэмпа-Месси.

Расширенный (4096, 2048)-код Рида-Соломона над GF (2) имеет скорость, равную 1/2, и позволяет исправлять все конфигурации ошибок из 1024 12-битоБых байтов. В типичных случаях алгоритм Берлекэмпа-Месси содержит 2f (или 2 097 152) умножений 12-битоБых чисел поля GF (2), а для наихудших конфигураций ошибок это число может возрасти в 1,5 раза. Ускоренный алгоритм позволяет провести вычисления лучше.

Подсчитаем число операций для несколько видоизмененного варианта ускоренного алгоритма Берлекэмпа-Месси. Вместо того чтобы формировать пакеты одинакового объема, делая разветвления алгоритма через каждые т итераций, будем строить разветвления в те моменты, когда степень многочлена Л (х) достигнет предписанного предела. А именно будем формировать новую ветвь алгоритма тогда, когда степень одного из многочленов, входящих Б матрицу А {х), станет равной 128, и закончим процесс формирования ветвей после 2048 итераций. В случае когда происходит точно 1024 ошибки, алгоритм будет содержать восемь разветвлений, каждое из которых будет выполнять 128 итераций. Имецро этот случай мы сейчас проанализируем.

В течение каждой итерации требующееся для выполнения вычислений, показанных слева на рис. 11.7, число умножений примерно вчетверо больше степени многочлена А [х), вычисляемого при этой итерации. Это вдвое больше числа умножений, необходимых в исходном варианте алгоритма Берлекэмпа-Месси. Следовательно, в каждом ответвлении алгоритма имеется примерно т итераций, выполняющих вычисления, указанные на левой части рис. 11.7. Всего имеется восемь ветвей, и т равно 128; таким образом, выполнение всех ветвей алгоритма содержит 524 228 умножений. К этому надо прибавить число умножений, необходимых для вычисления указанных в правой части рис. 11.7 сверток, объединяющих вычисленные пакеты. Для вычисления этих линейных сверток воспользуемся алгоритмом 315-точечной циклической свертки, содержащим 2470 умножений. Этот алгоритм представляет собой алгоритм Агарвала-Кули вычисления свертки, построенной из трех алгоритмов вычисления коротких сверток, длины которых соответственно равны пяти, семи и девяти.

После каждого ответвления надо вычислять член вида А {x)S{x), где степень многочлена 5 {х) равна 2048 кх, а степень многочлена Л [х) равна 128. Воспользуемся методом перекрытия с на-комплением и алгоритмом 315-точечной циклической свертки. Это даст нам 315 - deg А (х) = 187 правильных выходных точек линейной свертки А (х) S [х). Для вычисления 2048- 256 точек алгоритм циклической свертки придется применить 10 раз. Так как Л {х) S {х) содержит четыре линейные свертки, всего потребуется 40 обращений к алгоритму циклической свертки.

Продолжая таким образом, всего получим 168 обращений к алгоритму циклической свертки, что в итоге дает 480 480 умножений.

После выполнения каждого пакета из 128 итераций необходимо также вычислить матричное произведение Л (х) Л (х). Разбивая в матричном произведении длинные свертки на короткие и проводя вычисления, аналогичные проделанным, приходим к 216-кратному обращению к алгоритму 315-точечной циклической свертки.

Полное число умножений, необходимых для рассматриваемого декодирования (4096, 2048)-кода Рида-Соломона, получается сложением этих трех величин. Всего получаем 1 462 768 умножений против 2 097 152 необходимых при непосредственном использовании алгоритма Берлекэмпа-Месси.

П,7, РЕКУРРЕНТНЫЙ АЛГОРИТМ БЕРЛЕКЭМПА-МЕССИ

Можно построить декодер, еще более эффективный, чем рассмотренный в предыдущем параграфе. Такой улучшенный декодер представляет не только практический,но и теоретический интерес, так как позволяет доказать, что асимптотическая сложность декодирования кодов Рида-Соломона не превосходит величины О (п log п) (и очень близка к величине О (п log п)). Этот алгоритм не только обладает хорошими асимптотическими свойствами, но и практически пригоден для кодов с умеренной длиной.

Для простоты в основном будем рассматривать случай, когда 2/ равно степени двух. Пусть длина 2t = 2р. Рекуррентный алгоритм сводит задачу длины 2 к двум задачам длины 2Р~\ которые сочленяются с помощью алгоритма 2-точечной свертки. Каждая из этих двух подзадач в свою очередь расщепляется на две подзадачи. Это продолжается до тех пор, пока не получается задача, состоящая из одной итерации. Если каждая подзадача аналогична исходной задаче, то алгоритм допускает рекуррентную реализацию.

В случае, когда 2t не является степенью двух, имеется несколько способов модификации процедуры. Один из них состоит в представлении числа 2t в виде произведения простых множителей. Если pi представляет собой /-й множитель, то на 1-м уровне задача подразделяется на pi подзадач вместо двух. В остальном алгоритм не меняется.

Второй способ состоит в замене числа итераций наименьшей степенью двух, превосходящей число 2t, и разбиении задачи на каждом уровне пополам. В каждый момент обращения к процедуре проверяется, превысил ли счетчик общего числа операций величину 2t. Если превысил, то итерация не выполняется и алго-