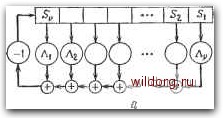S(x)

Коэффициенты в отвойах ровны Лу

На11йльное состояние регистра

S(x)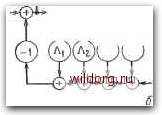

Коэффициенты в отвойах равны Л.у

Рис. 7.4. Генграция спектра ошибок, а - вариант Месси; б - вариант Берлекэмпа.

что Aj = О При / > t. Удовлетворяющий этому равенству вектор Л определяет коэффициенты многочлена локаторов ошибок

Л(х) = П(1-0,

где Xi, /= 1, V, являются локаторами ошибок. Многочлен значений ошибок не вычисляется с помощью этого алгоритма, но получается позже из А (х) и 5 (х) согласно определению Q (х) = S (х)Л(х) (modxO-

Вариант Берлекэмпа решения этой задачи показан на рис. 7.4,6, из которого видно, что многочлену значений ошибок отводится центральная роль. Такой вариант предполагает поиск векторов Л и й, компоненты которых равны нулю при t < k п и удовлетворяют 2t уравнениям t

Sj+ Ii Sj nA„ = Qj, /=1.....2/,

где Sj = О при / < 0. Заметим, что / пробегает 2t значений. Решение задачи дается двумя многочленами: многочленом локаторов ошибок и многочленом значений ошибок.

Два описанных выше варианта эквивалентны. В дальнейшем будет рассмотрен вариант, предложенный Месси. При необходи-

Начальное состояние регистра

Начальные значения:

А(х)=\, г = 0 1 = 0, В(х) = \

Вычисление сшибки в слеВрщеО к,омпонен1Т1е сикЗрома i=i j=G

Генерирует ли существующий регистр сВЕига слеВующую компоненту синорома?

Да;отбоВы оБратной связи остаются 5ез изменения

Hem; отвойы обратной связи неоБхоВимо изменить

Вычислить новый многочлен связей, Вля которого Дг = 0

T(x)=A(x)-trXB(x)

НаВо ли увеличивать Влину регистра?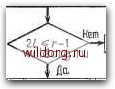

А{х)-Т(х)

В(х)АгА(х) Сохранение прежнего регистра

после нормализации A(x).Tfx) МоВифУкация регистра сВвига L -r-L Изменение Влины

В(х)*-хВ(х)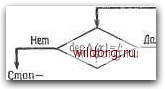

6 принятом слове более t ошибок,

К слеЗующему этапу йекоВированУЯ

Рис. 7.5. Алгоритм Берлекэмпа-Месси,

МОСТИ алгоритм Берлекэмпа-Месси можно преобразовать в форму Берлекэмпа, производя итерации непосредственно для многочленов Л() (х) и Q(> (х).

На рис. 7.5 приведена блок-схема алгоритма Берлекэмпа- Месси. Как было показано, этот алгоритм позволяет вычислять многочлен локаторов ошибок исходя из заданных 2t компонент

Таблица 7.3

Алгоритм Берлекэмпа-Месси для (15, 9)-кода Рида-Соломона, исправляющего тройные ошибки

й(х) = (х- + aK-t + а-Чх + oLx + a*X.v + « + )

(А) = 0

lix) = xv + ах + а" .х = fix)

.Sj = +я v» + a"a* = I

S.i = aa"+«V° + «"a«

с Д, Т(\) В(х) Л(л) L

0 11 О

1 а" l+ax а 1

2 а \+а\ ах 1+а-\х 1

3 I l+ax + ax 1+ах 1+ах + ах 2

4 1 1+а*л- x + aV l+o(*.v 2

5 а" 1+а"*х+э("л- + а"х «* + ах 1 + аЧ + я"л-+!(*л i

6 О I+а*.х + а".х + а*.х- а\х + ах I+=(.x + я"л+ «"х"

Л(.х)= 1 +я*х + я".х + я*х=(1 +ях)(1 +x\vl(l fslv)

синдрома Si, Sit- Если jo в коде отлично от 1, то определим S, =V7+/o-i. у = 1, 2/. Эти компоненты синдрома участвуют в вычислениях точно так же, как и прежние компоненты. Сам алгоритм при этом не претерпевает никаких изменений, и дело сводится лишь к соответствующему изменению индексов внутренних переменных в алгоритме.

Этот алгоритм и его обоснование будут понятнее, если во всех деталях проследить работу алгоритма по схеме на рис. 7.5 для конкретных примеров. В табл. 7.3 приведены необходимые вычисления для (15,9)-кода Рида-Соломона, исправляющего тройные ошибки. В достоверности приведенных вычислений можно убедиться, проделав шесть итераций по изображенной на рис. 7.5 схеме. Табл. ТЛ содержит аналогичные вычисления для исправляющего тройные ошибки (15,5)-кода БЧХ.

Внутренняя логика работы алгоритма Берлекэмпа-Месси может показаться несколько загадочной. Возможно, ответы на