1) Стековая память (push-down stack) - устройство памяти, считывание данных из которой начинается с вершины и производится в порядке, обратном порядку записи («пришел последним - обслуживается первым»).-Прим. перев.

ритм декодирования переходит к своему следующему шагу. В остальном алгоритм не изменяется.

Формулировка шага рекуррентной процедуры становится очевидной, если заметить, что описанные в предыдущем параграфе вычисления величин и ас- по величине S" (х) в точности совпадают с процедурой теоремы 7.4.1 с заменой 2t на т, Л) (х) на Л*- (х) и вектора синдромных многочленов S (х) на S**) (х). Следовательно, для вычисления ас- *> (х) можно воспользоваться тем же алгоритмом, что и для вычисления Л(2) (х).

Этот рекуррентный алгоритм, названный процедурой БерМес, приведен нарис. 11.8. Процедура использует самое себя. Она содержит сте*коБую память ), в которой при переходе с одного уровня на другой временно запоминаются данные одного уровня. Поведение алгоритма на следующем уровне ничем не отличается от его поведения на предыдущем уровне, но в стеке записываются другие данные. В конце концов задача сводится только к одной итерации, и ge уже нельзя разделить пополам. Тогда процедура БерМес состоит просто в выполнении этой итерации и алгоритм возвращается в надлежащую точку.

Каждый раз при обращении процедуры БерМес к самой себе необходимо запоминание локальных переменных в стеке. Если Б начале алгоритма решение задачи требует 2р итераций, то глубина рекурсии равна р: имеется р уровней рекуррентного алгоритма. Объем стека должен быть достаточно велик для того, чтобы содержать все временные множества переменных.

Алгоритм проходит /-Й уровень 2Р раз: нулевой уровень - один раз, первый уровень - два раза и т. д.; последний уровень проходится 2Р раз. Выполняемое на t-м уровне вычисление S(x)

Л (х) S (х) содержит четыре умножения многочленов. Степень многочленов Л (х) равна примерно 2р~~ - 1, и они умножаются на многочлены степени 2p~+i - i. Необходимо правильно вычислить только 2Р~ коэффициентов произведения многочленов, а именно коэффициенты, стоящие при степенях переменной от х~ до х-~~~, так как только эти коэффициенты входят Б вектор S (х), используемый при втором обращении к процедуре БерМес. На /-м уровне вычисляется также матричное произведение Л (х) Л (х), которое содержит произведения многочленов степени 2P~~ каждый.

Число умножений в процедуре БерМес почти полностью определяется свертками, так как итерации алгоритма Берлекэмпа -

I Обращение к процейуре БерМес

1-

Стоп

Вхой в процейуру БерМес i

Запись копий многочленов Sixj и К(х)

Аг,-Д-:Дг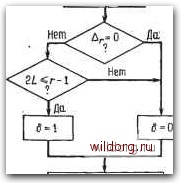

L 6{r-L)-(\-d)L

I -йгХ

6 (\-В)х.

Выталкивание копой многочленов s(x) U aix)

Обращение к процейуре берМес

Обращение к процейуре БерМес

/<{х)-К(х)А(х)

Выхой из процейуры БерМес Рис. 11.8. Процедура БерМес.

Рис. п.9. Подсчет числа умножений в процедуре БерМес.

Месси фактически выполняются только на конечном шаге, на котором все подалгоритмы алгоритма содержат по одной итерации и только по одному умножению (на Дш), которым при подсчете общего числа умножений можно пренебречь. Вычислительная сложность процедуры БерМес определяется непосредственно вычислительной сложностью алгоритмов свертки. Успех ее использования предполагает наличие хорошего набора алгоритмов свертки.

На рис. II.р приведены результаты подсчета числа умножений Б рекуррентном алгоритме декодирования применительно к тому же (4096, 2048)-коду Рида-Соломона, который был рассмотрен в предыдущем параграфе. Для вычисления циклических сверток Б обеих половинах использовались метод перекрытия с накоплением и одна из коротких сверток, приведенных на рис. П.5. Выписанные на рис. 11.9 детали расчетов являются убедительным свидетельством сложности структуры рассматриваемого алгоритма. Эта структура, однако, позволяет разумно использовать вычислительные ресурсы при программной и аппаратурной реализации отдельных фрагментов. По мере необходимости она вызывает алгоритмы свертки из библиотеки таких алгоритмов.

В общем случае алгоритм Берлекэмпа-Месси, содержащий 2t итераций, имеет измеряемую числом умножений вычислительную сложность порядка (logg 2t) С (t), где С {{) - число умножений, необходимое для вычисления свертки двух многочленов степени t. Это объясняется тем, что к /-му уровню алгоритм обращается 2 раз, причем длина выполняемой на 1-м уровне свертки равна 2~t. Сложность вычисления 2 сверток длины 2~Ч каждая