Дребовийные ко8ы

Линейные

Линейные врееовианые кобы

Сисглематические

Систематические линейные Оревовийные койы

С конечной йлиной койоеого ограничения U постоянные во бремени

С конечной йлиной койоеого ограничения

Решетчатые

КО0Ы

С конечной йлиной койоеого ограничения U постоянные 60 времени

Систематические

Постоянные во времени

Систематические решетчатые койы

Скользяиие блоковые койы

Линейные

Систематические

Сверточные кобы

Постоянные во времени

Систематические скользяш,ие блоковые койы

Система,-тические „

Линейные

Систематические сверточные койы

Рис. 12.2. Классификация древовидных кодов.

В буфер по одному символу в единицу времени с каждого выхода; их считывание из буфера производится вдвое чаще, чем поступают входные символы.

Сверточные и другие решетчатые коды удобно описывать специальным графом, называемым решеткой; отсюда название - решетчатые коды. Решеткой называется граф, узлы которого находятся в прямоугольной координатной сетке, полубесконечной справа; число узлов в каждом столбце конечно. Конфигурация ребер, соединяющих узлы каждого столбца с узлами столбца справа, одинакова для всех столбцов. Узлы, которые не могут быть достигнуты при движении вправо из верхнего левого узла, обычно не указываются.

Информационные Биты

КоЭоеые биты

<±>-к±ь

Уйвоенная тактовая скорость

Информационные биты

КоЭовые биты

( + б

Уйвоенная тактовая скорость

Рис. 12.3. Примеры сверточных кодеров, а - кодер для двоичного сверточного (12, 6)-кода; б - кодер для двоичного сверточного (6. 3)-кода.

Типичная решетка для двоичного кодового алфавита представлена на рис. 12.4. Эту решетку можно использовать для описания второго кодера, изображенного на рис. 12.3. Ее маркировка на рис. 12.5 соответствует этому кодеру. Узлы в каждом столбце решетки представляют q состояний, в которых может находиться регистр сдвига. Каждый последуюш,ий столбец представляет собой набор состояний в следующий момент времени.

Поступление на вход нового кадра приводит к изменению состояния регистра сдвига, соответствующему ребру, которое ведет к следующему узлу. В нашем примере каждое ребро помечено двумя двоичными символами, передаваемыми в канал при переходе в следующее состояние регистра сдвига. В том простом примере, который мы рассматриваем, ведущая из произвольного узла верхняя прямая соответствует нулевому входному двоичному символу, а нижняя - единичному. В общем же случае каждое ребро помечается kf, входными символами, которые ему соответствуют.

Маркированная решетка описывает сверточный код в том смысле, что все пути слева направо по решетке обозначают кодовые слова. Маркировка ребер одинакова для каждого сегмента и линейна в том смысле, что линейная комбинация маркировок любого множества ребер является маркировкой некоторого ребра.

Решетка может быть маркирована и при более слабых ограничениях. Если маркировка не обладает свойством линейности, то, как мы уже указывали, код называется скользящим блоковым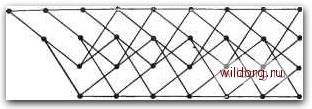

Рис. 12-4. Решетка сверточного кода Время

Состояние О 1

г 3 00 00 00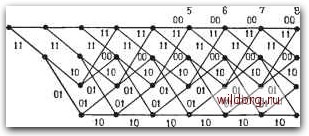

00 1С 01 И

Послейний поступивший Бит

Рис. 12.5. Решетчатая диаграмма сверточного (6, 3)-кода.

КОДОМ. Если маркировка меняется от кадра к кадру, то такой код известен под общим названием решетчатого кода. Наконец, если число состояний в следующих друг за другом временных кадрах продолжает неограниченно расти, то такой код называется общим древовидным кодом.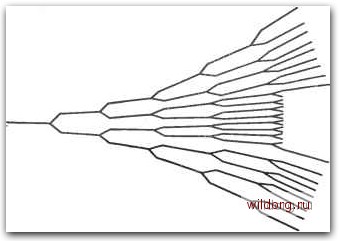

Рис. 12.6. Дерево для двоичного древовидного кода со скоростью 1/2.