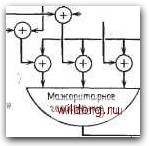Рис. 13.1. Мажоритарный декодер для симплексного (7, 3)-кода.

Конечно, для исправления одной ошибки необходимо использовать лишь два из приведенных выше проверочных равенств. Добавление третьего равенства приводит к декодеру, основанному на правиле решения «два из трех», а не на правиле «два из двух». До тех пор пока происходят одиночные ошибки, оба декодера ведут себя одинаково, но, если произошло две ошибки, поведение декодеров становится различным. Декодер «два из трех» исправляет несколько большую долю конфигураций из двух ошибок, хотя оба декодера не исправляют или неправильно исправляюг большинство конфигураций из двух ошибок. При желании можно потребовать, чтобы удовлетворялись все три проверочных равенства. Тогда декодер будет исправлять всеодиночные и обнаруживать все двойные ошибки.

Можно превратить мажоритарный декодер в декодер Меггитта. Напомним, что синдромный многочлен определялся или как

S {Х) = Rg (;,) [V (х)],

или как

six) = Rs(.) [х-" V (х)].

Через проверочную матрицу синдромный многочлен линейно связан с принятым многочленом v (х). Запишем каждый коэффициент в виде

Sj = Ti Hifi, j = 0, .., n-k-l.

Любое другое проверочное равенство получается как некоторая линейная комбинация строк Н, т. е. как линейная комбинация компонент синдрома. Поэтому все проверочные соотношения,

[So Si Sg S3] = [Vo Ui V2 i Vb Ve]

используемые мажоритарным декодером, могут быть получены как линейная комбинация коэффициентов синдрома декодера Меггитта. Таким образом, любой мажоритарный декодер для циклического кода может быть реализован как декодер Меггитта.

Симплексный (7,3)-код является циклическим, и его порождающий многочлен равен (л;) = х + + х + 1. Пусть

= v,x + v.x + vx -f Vs + Da + X + 1) + vi (x + + x) +

Это соотношение можно переписать в виде

- 1 1 1 О 0 111 110 1 10 0 0 0 10 0 0 0 10 0 0 0 1

Для мажоритарного декодирования будем использовать следующие проверочные равенства:

Со + Cl -Ь Св = О, Со + Сг -Ь Сз = О, Со + С4 -Ь Со = 0.

Выражение в левой части первого из них совпадает с Sg, второе - с So, а третье - с Si -f Sg. На рис. 13.2 показан мажоритарный декодер, реализованный как декодер Меггитта.

Мажоритарные декодеры даже без каких-либо дополнительных модификаций декодируют много ошибочных конфигураций и вне радиуса упаковки кода. Это может показаться заманчивым преимуществом мажоритарных декодеров. Однако, как правило, мажоритарное декодирование применяется для кодов, у которых радиус упаковки мал по сравнению с другими кодами с сопоставимыми скоростью и длиной. Способность декодера декодировать вне радиуса упаковки можно рассматривать лишь как частичную компенсацию за выбор кода с худшими характеристиками.

Для того чтобы мажоритарный декодер, реализованный как декодер Меггитта, исправлял большое число конфигураций ошибок вне радиуса упаковки, необходимо добавить цепь обратной

4Б6 гЛ. 1з. декодирование мажоритарным метОдОМ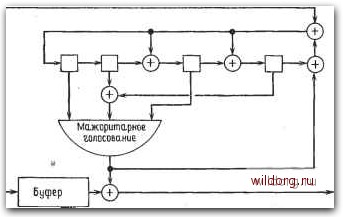

Обратная связь

Рис. 13.2. Декодер Меггитта для симплексного (7, 3)-кода.

связи; такая "цепь показана на рис. 13.2. Если декодирование вне радиуса упаковки не играет особой роли, то цепь обратной связи можно опустить.

13.3. АФФИННЫЕ ПЕРЕСТАНОВКИ ДЛЯ ЦИКЛИЧЕСКИХ КОДОВ

Циклический сдвиг любого кодового слова в циклическом коде дает другое кодовое слово. Следовательно, весь код инвариантен относительно циклического сдвига. Циклический сдвиг является простым примером перестановки. Циклический кодТможет быть инвариантен и относительно других перестановок. В этом параграфе мы покажем, что многие циклические коды, будучи расширенными, становятся инвариантными относительно большой группы перестановок, называемых аффинными. Аффинные перестановки могут использоваться для построения кодов, для их исследования или для построения декодеров, в частности мажоритарных.

Пусть - циклический код длины п = q"" - 1, порождаемый многочленом g{x), и пусть - код длины q", получаемый из добавлением к каждому кодовому слову символа проверки на четность. Иначе говоря, если Cj, Cq) - кодовое слово

в ё, то (с„ 1, Су, Со, Соо) - кодовое слово в здесь Соо - символ проверки на четность, определяемый как См = ~{Cn-i + + . + Ci + Со).

Чтобы перенумеровать компоненты кодового слова, будем использовать GF (q") как множество локаторов. Ненулевые элементы GF (q") суть а, где а - примитивный элемент. Нулевой