в третьем регистре сдвига. В схеме последовательного исполнения для выполнения сложения требуются четыре такта, а в схеме параллельного исполнения требуется только один такт, но сумматор содержит больше проводов и сумматоров по модулю 2. При желании слагаемые могут быть возвраш,ены в исходные регистры сдвига для дальнейшего использования в других целях.

На рис. 6.5 изображен умножитель произвольного элемента поля GF (16) на константу р = поля GF (16). Для описания этого устройства нам необходимо конкретизировать представление поля GF (16). Предположим, что оно построено с помош,ью примитивного многочлена р (z) = + z + 1 и что у = yz + yz + + Уг + То - произвольный элемент поля. Тогда

РТ = Узг + У, + Угг + То =

= (Тз + То) + (Тз + Уд + (Та + Ti) Z + Ti-

Из этого равенства непосредственно вытекает способ параллельного исполнения умножителя на скаляр. Последовательное исполнение этого умножителя менее очевидно. В нем использованы обе строки предыдушего равенства: сначала вычисляется -ygz" + + У2 + Ti2* + То, а затем делается приведение по модулю Z* -Ь Z + 1. Эта схема является цепью деления на многочлен Z* -Ь Z + 1. Для выполнения умножения на р в ней требуются четыре такта.

6.2. ЦИФРОВЫЕ ФИЛЬТРЫ

Регистры сдвига можно использовать для умножения и деления многочленов над GF (q); этим и объясняется их частое применение в конструкциях кодеров и декодеров. Регистры сдвига полезны и для развития теории, так как играют роль своего рода псевдоматематических обозначений, помогаюш,их лучше понять некоторые действия над многочленами. Цепи регистров сдвига называются также фильтрами.

Можно интерпретировать п символов, содержащихся в регистре длины п, как коэффициенты многочлена степени п -1. В качестве обычного соглашения условимся, что регистр всегда сдвигается слева направо. Такое требование приведет иногда к тому, что коэффициенты многочлена будут появляться в регистре сдвига в нисходящем порядке справа налево, а это, к сожалению, противоречит общепринятому правилу записи многочленов.

Для циклического сдвига многочлена используется замкнутый в кольцо регистр сдвига. На рис. 6.6 изображен «-разрядный регистр, используемый для циклического сдвига многочлена степени /г - 1. Он вычисляет xv {х) (mod х" -]). Это простейший пример регистра сдвига с линейной обратной связью.

Рис. 6.6. Устройство циклического сдвига многочлена.

Рис. 6.7. Регистр сдвига с линейной обратной связью.

Общий ВИД регистра сдвига с линейной обратной связью показан на рис. 6.7. Эта цепь реализует вычисление рекурсии

Pj = - Ii hiPj-i, iL.

Если в начальный момент регистр загружен L символами {pQ, > Рьг), то на выходе регистра появится бесконечная последовательность символов, начинающаяся с ро я удовлетворяющая выписанному выше рекуррентному уравнению. Если этот фильтр используется в изображенной на рис. 6.8 цепи, то он называется авторегрессионным фильтром. Так как в нем имеется обратная связь, то он относится к обширному классу так называемых рекуррентных фильтров.

Вместо того чтобы на вход фильтра подавать по линии обратной связи его выходной сигнал, в качестве входного сигнала можно использовать генерируемую извне последовательность. Такой линейный регистр сдвига без обратной связи показан на рис. 6.9. Он называется также фильтром с конечным импульсным откликом (КИО-фильтром) или нерекуррентным фшльтром.

Пусть коэффициенты многочлена g {х) = gx + ... + gx -f -Ь go равны весовым множителям в отводах регистра сдвига без обратной связи, и пусть входная и выходная последовательности записываются соответственно многочленами а {х) аих + ... -f -Ь ах + Оо и (х) = bfe+LX* -Ь ... + ЪуХ + bo- Тогда произведение этих многочленов b {х) = g {х) а {х) описывает происходящие в изображенном на рис. 6.9 регистре сдвига процессы при условии, что в начальный момент регистр содержал только нули и ввод элемента Uq сопровождается вводом L нулей. Говорят,

что коэффициенты многочленов а (х) м g (х) свертываются регистром сдвига, так как

bj = И giaj t.

Применительно к многочленам КИО-фильтр можно рассматривать как устройство для умножения произвольного многочлена а {х) на фиксированный многочлен g {х). Мы будем называть его также цепью умножения на g {х).

На рис. 6.10, а приведен пример цепи умножения на g (х) для g{x) = = г* + + х* Ч- л; -f х -f-1. Эта цепь является КИО-фильтром. Подчеркнем, что внутренние разряды регистра сдвига считываются, но не изменяются. Можно указать другой вариант устройства, в котором внутренние разряды меняются, но, как правило, этот альтернативный вариант оказывается более дорогим. На рис. 6.10, б показан такой альтернативный вариант для цепи умножения на g {х). Эта форма КИО-фильтра не является общепринятой.

Регистр сдвига можно также использовать для деления произвольного многочлена на фиксированный многочлен. Выполняющая эту операцию цепь почти повторяет обычную процедуру де-

Рис. 6.8. Авторегрессионный фильтр.

Pvh-Pi-Po

.6, ••..6i.Jt-l.*i+t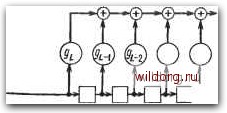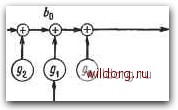

Рис. 6.9. Регистр сдвига без обратной связи.