Начало:

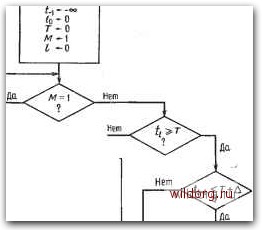Если возможно, то увеличить попевнии информационный ковр Положить

В противном случае йвигаться назай Положить

Буфер перепопнен, жйать нового начала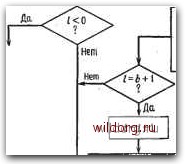

Начать новый информационный кайр с первого значения

Если возможно,

уменьшить и 7", и

на величину, кратную Д

Рис. 12.28. Алгоритм Фано.

перенастроиться. Если вероятность того, что на длине блока не произойдет ошибок, не слишком мала, то декодер, предполагая, что ошибок нет, преобразует кодовое слово в информационное слово. Если код систематический, то это делается непосредственно; в противном случае необходимо применить китайскую теорему об остатках для многочленов. Если длина свободного от ошибок сегмента принятого слова равна длине кодового ограничения, то

декодер находит правильный узел и продолжает декодирование. Если в противоречии с нашим предположением появилась ошибка, то узел неправилен, и буфер скоро снова переполнится. Этот процесс продвижения декодера вперед продолжается до тех пор, пока не будет получено правильное декодирование.

ЗАДАЧИ

12.1.а. Построить кодер для систематического некатастрофического деоич-ного сверточного (16, 4)-кода с минимальным расстоянием d* = 9 и длиной кодового ограничения v = 3.

б. Чему равно свободное расстояние этого кода?

12.2. Каждый код Хэмминга над GF (q) может быть использован для построения сверточного кода над GF (q), исправляющего одну ошибку.

а. Построить проверочную матрицу систематического восьмеричного (9, 7)-кода Хэмминга.

б. Основываясь на этом коде Хэмминга, найти проверочную матрицу (30, 27)-кода Вайнера-Эша над GF (8).

в. Построить кодер и синдромный декодер.

г. Чему равна скорость этого кода? Чему равна скорость шестна-дцатернчного кеда Вайнера-Эша, основанного на (17, 15)-коде Хэмминга над GF (16)?

12.3. Построить кодер (12, 9)-кода Вайнера-Эша, использующий один двоичный регистр сдвига длины 3.

12.4. Построить кодер и синдромныйдекодер для (32, 28)-кода Вайнера- Эша.

12.5. Снова рассмотреть пример, приведенный на рис. 12.25, используя в качестве принятого слова

V = 10001000001000000000... .

12.6. Определить, какие из перечисленных ниже сверточных кодов со скоростью 1/2 являются катастрофическими:

а. gy{x) = x\ е2(х) = +х+ 1.

б. g{x) = х+ х+ \, g{x)x++x+\.

в. gy{x) = +-1+х+ 1, й W = xf+x+\.

г. gy{x) = xf>+x. + x+\, g{x) = x. + +x+\.

12.7. Сверточный код со скоростью- 1/3 и длиной кодового ограничения 2 имеет порождающие многочлены gi(x) - хх-\- \, g(x) = х-\-х-\- \, ёз (х)= x-i- I и doo, равное 8.

а. Чему равно минимальное расстояние этого кода?

б. Чему должна быть равна ширина окна декодирования для исправления всех тройных ошибок?

в. Построить исправляющий все двойные ошибки декодер для этого кода с шириной окна декодирования, равной 9.

12.8. Сверточный код над GF (4) со скоростью 1/2 имеет порождающие многочлены gi (х) 2л: + 2д;= + 1 и gs (х) = х+ I.

а. Показать, что этот код не является катастрофическим.

б. Показать, что его минимальное расстояние равно 5.

в. Сколько конфигураций из двух ошибок располагаются на длине ограничения декодирования, равной 8?

ЗАМЕЧАНИЙ 44?

Г. Построить синдромный декодер для исправления всех двойных

ошибок.

12.9. Найти систематический кодер е регистром сдвига и с обратной связью для двоичного сверточного кода с порождающей матрицей

G(x) =

X х 1 о 1 X

ЗАМЕЧАНИЯ

Понятие сверточного кода было введено Элайсом [1954] и развито Возенкрафтом [1957]. Вайнер и Эш [1963] предложили для семейства сверточных кодов, исправляющих одну ошибку, общую конструкцию, родственную конструкции кодов Хэмминга. Класс сверточных кодов, исправляющих многократные ошибки, нашел Месси [1963]. Коды Месси просты в декодировании, но в то же время имеют не слишком хорошие характеристики. Общего правила построения семейства быстродействующих высококачественных сверточных кодов, исправляющих многократные ошибки, не известно. Костелло [1969] предложил некоторые пути нахождения хороших сверточных кодов с умеренной длиной блока. Основные используемые в настоящее время коды были найдены поиском на ЭВМ Буссгангом [1965], Оденвальдером [1970], Болом и Джелинеком [1971], Лар-сеном [1973], Пааске [1974] и Йоханнессоном [1975]. Эти коды приведены на рис. 12.13.

Общее исследование алгебраической структуры сверточных кодов было проведено Месси и Сайном [1968], а также Форни [1970], который впервые использовал решетки. Наше описание таких кодов с помощью многочленов основывается на этих статьях. Костелло [1969] показал, что если в кодере введена обратная связь, то каждый сверточный код можно свести к систематическому. Дополнительное обсуждение абстрактных структур может быть найдено у Линднера и Штайгера [1977].

Создание декодеров для сверточных кодов начали со сложных декодеров с хорошими характеристиками, а затем постепенно перешли к простым декодерам с посредственными характеристиками, которые так популярны теперь. Алгоритм поиска на решетке принадлежит Фано [1963]. Наша формулировка алгоритма Фано следует Галлагеру [1968] и сильно отличается от первоначальной. Витерби [1967] предложил свой алгоритм скорее в учебных целях, чем в качестве серьезного алгоритма. Вскоре после этого Хеллер [1968] указал, что алгоритм Витерби при не слишком больших длинах кодового ограничения вполне практичен.

Общее обсуждение сверточных кодов можно найти в книге Витерби и Омуры [1970], а также в обзорных статьях Форни [1974] и Месси [1975].