Итак, если в качестве начальной точки в алгоритме Берлекэмпа- Месси вместо 1 выбрать многочлен ¥ (х), то модифицированный синдром вычисляется неявно и нет необходимости вводить его в явном виде. Отбросим теперь обозначение Л (х), заменив его на Л (х) и назвав многочленом локаторов ошибок и стираний. При начальных условиях, даваемых многочленом (х), алгоритм Берлекэмпа-Месси рекуррентно порождает многочлен локаторов ошибок и стираний в соответствии с уравнениями

Л> (х) = Л"-> (х) - Д,хБ-" (х).

ВЧ (х) = (1 - б,)хВ-" (X) + 6,АГЛ~ W.

Дополненный правилами восстановления стираний алгоритм Берлекэмпа-Месси приведен на рис. 9.4. Сопоставим его с алгоритмом на рис. 9.1. Единственное изменение по сравнению с алгоритмом для исправления только ошибок состоит в вычислении многочлена локаторов стираний; сравнительно с остальными вычислениями алгоритма оно является тривиальным. Это вычисление производится с помощью показанной на рис. 9.4 специальной вспомогательной цепи, содержащей первые р итераций. Индекс г используется в качестве счетчика для первых р итераций, а после вычисления многочлена стираний в качестве счетчика последующих итераций алгоритма Берлекэмпа-Месси до тех пор, пока г не превзойдет 2t. При каждом стирании длина L регистра сдвига возрастает на единицу, а затем изменяется в соответствии с обычными правилами процедуры алгоритма Берлекэмпа-Месси. Поскольку, однако, этот алгоритм не учитывал стираний, то в конце приходится добавить исправления стираний и заменить г и L на г - р и L - р соответственно.

Прежде чем закончить данныйпараграф, заметим, что вместо пробела, обозначающего стирание, можно оставить лучше всего угаданный символ, пометив факт наличия в данной компоненте стирания некоторым специальным образом. Такие стирания назовем помеченными. Эти позиции не влияют на алгоритм декодирования, так как стоящие в них символы заменяются нулями. Иногда вне основного декодера удается использовать дополнительные блоки, извлекающие пользу из этой слабой информации. Наприме, , можно отказаться от полученного на выходе декодера слова, если слишком многие из помеченных стираний не совпадают с результатом декодирования.

9.3. РАСШИРЕННЫЕ КОДЫ РИДА-СОЛОМОНА 299

Начальные значения; /.=г = 0

Л(ж)-Aix) -nxAix) В(х) ~А{Х) L-L+1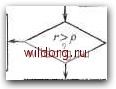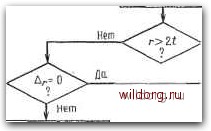

ja-число стираний г/-локатор Z-го стирания

Вычисление нового многочлена связей. Зля которого Др = 0 Дх) ~А[х) - AxBto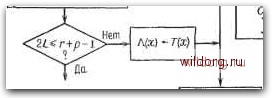

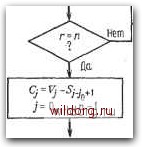Стоп

B<?i)-xB(x)

Рис. 9.4. Исправляющий ошибки и стирания декодер для кодов БЧХ.

9.3. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ

РИДА-СОЛОМОНА

Незначительная модификация любого декодера для кода Рида-Соломона позволяет получить декодер для расширенного кода Рида-Соломона. Один из возможных способов состоит просто

) В случае расширения кода на два символа удобно изменить нашу обычную индексацию и обозначить компоненты синдрома через So, St-i-

В переборе всех возможных значений ошибок в двух символах расширения и последующих попытках декодирования для каждой пары. Если такая попытка приводит к кодовому слову при или менее исправлениях, то результат правилен, так как только одно кодовое слово находится на расстоянии от принятого слова.

Лучше, однако, отдельно рассматривать два случая возможных конфигураций ошибок: в первом случае искажен хотя бы один из символов расширения, а во втором ошибок в символах расширения нет. Сообщение при этом декодируется дважды (для каждого из случаев по отдельности). Пусть ) S,= при

/== 1, 2t- 2, и пусть So У/„ - t) и Sg-i -= Vj+zt-i - v, если v и не искажены. В первом случае во внутреннем векторе происходит rife более t - 1 ошибок и поэтому 2-2 компонент синдрома Si, S2t 2 достаточно для того, чтобы правильно восстановить внутренний спектр конфигурации ошибок. Эти 2t-2 компонент синдрома можно рекуррентно продолжить до п - 2 компонент спектра конфигурации ошибок, так как S} = = Ejj. Во втором случае все ошибки лежат во внутреннем векторе, но их не более t, и поэтому для восстановления спектра конфигурации ошибок компонент достаточно 2t компонент So, S2t i. Вообще говоря, одной попытки декодирования недостаточно и приходится делать обе попытки но так как минимальное расстояние кода равно 2t-\-\, может быть найдена только одна конфигурация не более чем из t ошибок.

Чтобы не удваивать сложность декодера дублированием декодеров, опишем вариант разделения вычислений, который дает лишь незначительное увеличение сложности. В этом параграфе мы опишем модификацию алгоритма Берлекэмпа-А1есси для декодирования расширенных кодов Рида-Соломона, а в следующем сделаем то же самое для расширенных кодов БЧХ. Ограничимся вычислением многочлена локаторов ошибок, так как остальные шаги алгоритма нам уже известны.

Наиболее важными расширениями кодов Рида-Соломона являются расширения на один символ, так как среди них содержатся коды плины 2", а во многих приложениях в качестве длины кода используется именно степень двойки. Мы начнем с этого случая, так как он представляет практический интерес из-за простоты декодера и так как его легко объяснить.

В рассматриваемом коде спектральные компоненты С/, ... ...,Су„ ) 2-2 равны нулю и единственную проверку на четность дает символ c L = С/„+2-1- Равенство нулю 2t- 1 компонент гарантирует, что минимальное расстояние в коде равно 2,и поэтому код позволяет исправлять t- 1 и обнаруживать ошибок. Блок