Окно ЙекоВироеания ДекоВер

Рис. 12.24. Наглядное представление работы декодера Витерби.

ными решениями декодера, но в случае некатастрофического кода декодер через короткое время обнаружит это.

Полезно представлять себе декодер Витерби как окно, через которое моЖно наблюдать часть решетки. Это иллюстрируется рис. 12.24. На рисунке можно видеть только часть решетки конечной длины, на которой отмечены выжившие пути. С течением времени решетка скользит влево - на практике довольно быстро. При появлении справа новых узлов некоторые пути продолжаются до них, а другие исчезают; самый старый столбец выходит из-под наблюдения налево. Со временем левый столбец узлов исчезает, и (при нормальной работе) лишь для одного из узлов этого столбца будет существовать проходящий через него путь.

На рис. 12.25 приведен пример работы алгоритма Витерби в случае сверточного (6,3)-кода с порождающими многочленами gy (х) = + X + 1 я g2 (х) = + I. Кодер для этого кода показан на рис. 12.3. Для простоты выберем в качестве информационной последовательности нулевую и (тоже для простоты) декодер с окном декодирования Ь, равным 15. Предположим, что

V = 10100000100000000000...;

это соответствует передаче нулевого кодового слова с тремя ошибками.

Диаграмма состояний декодера представлена на рис. 12.25. На третьей итерации декодер находит кратчайший путь к каждому узлу третьего кадра. Затем на г-й итерации декодер находит кратчайший путь к каждому узлу г-го кадра, продолжая пути, ведущие к узлам (г - 1)-го кадра и сохраняя кратчайший путь к каждому узлу.

Иногда может возникать неопределенность. В нашем примере имеются две неопределенности в пятой итерации. Декодер может либо разрешить неопределенность случайным образом, либо

10 10 10 10 =7lO 10 00 00 10 00 00 00 no 00.

Итерация 3

Итерачия k

0 12 3 4 5

Итерация 5

Итерация 6

Итерация 9

Итерация 10

• • •

о I 2 .1 4 5 6 7 8 9 101 1

Итерация 11

Итерация \1

• • «У» 6

О 1 2 3 4 5 6 7 8 О 10 11 12 13

Итерация 13

Итерация 7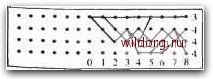

Итерация 14

Итерация 8

Рис. 12.25. Пример работы алгоритма Витерби.

Итерация 15

436 t-n. 12. сБЁРТОчмыЁ коды

сохранять оба пути, относительно которых существует нёонрё* деленность. В нашем примере неопределенности сохраняются до тех пор, пока не выявляется более правдоподобный путь или сомнительный участок не исчезает из поля зрения декодера.

По мере продвижения декодера к последующим кадрам из его памяти выводятся более ранние кадры. Если в самом старом кадре существует лишь один узел, через который проходит путь, то декодирование является полным. Если таких путей несколько, то принимается решение об обнаружении неисправляемой конфигурации ошибок. Она либо отмечается в качестве таковой, либо производится случайный выбор.

В нашем примере информационная последовательность может быть декодирована либо как

1 = 0 0 0 0 0 0 0...,

либо как

1 = 1 0 1 0 0 0 0 ....

Если сделать ширину окна декодирования более 15, то ошибка по-прежнему останется неисправляемой. Для исправления этой конфигурации ошибок требуется код с большим свободным расстоянием.

Декодер, символически изображенный на рис. 12.25, при практической реализации выглядит совершенно иначе. Например, выжившие пути через решетку представляются таблицей 15-битовых чисел. На каждой итерации некоторые 15-битовые числа сдвигаются влево, причем левый бит сбрасывается, а справа добавляется новый бит. Другие 15-битовые числа не наращиваются, а сбрасываются из таблицы.

По мере продвижения декодера накопленная мера расходимости увеличивается. Для того чтобы избежать проблемы переполнения, необходимо время от времени уменьшать эту меру. Простая процедура состоит в периодическом вычитании из всех мер расходимости наименьшей такой меры. Очевидно, что это не повлияет на выбор максимального расхождения.

В случае когда длина кодового ограничения мала, декодеры Витерби могут работать очень быстро. Например, практически возможно построить декодер со 128 узлами на каждом уровне, который производит 10 миллионов итераций в секунду.

12.9. АЛГОРИТМЫ ПОИСКА ПО РЕШЕТКЕ

Можно улучшить характеристики сверточного кода, увеличив длину кодового ограничения. Декодер Витерби, однако, быстро становится непрактичным: при длине кодового ограничения 10 декодер двоичного кода уже должен помнить 1024 выживших путей.