00) =

nl n - A

Al /1

аналогичное формуле потерь Эрланга. Вероятность того, что все п выводов заняты и обслуживания ожидают г вызовов,

РЛ->г) = Р{>0)(--у\ г = 0, 1,2,....

" а среднее число всех ожидающих вызовов

п - А

Вероятнасть Р(>0) конечна и при очень малом обмене. Чем ближе значение интенсивности поступающей нагрузки к числу выводов, тем больше число ожидающих вызовов, в то время как вероятность ожидания, так же как и Pw(>r), приближается к единице.

Вследствие экспоненциального распределения длительности занятия время ожидания имеет такое же распределение. Таким образом, вызов ожидает обработки в течение времени, большего t, с вероятностью

P{>t)P(>0)e "\

t>0

(рис. 6.14). Здесь tw=tm/n-А - среднее время ожидания для ожидающих вы310в0в. И при очень малой интенсивности поступающей нагрузки значение-w не меньше tm/n, так как если вызов вообще ожидает, то в среднем он должен ждать до тех пор, пока вывод не освободится. Среднее время ожидания t*w всех вызовов.

Рис. 6.14. Вероятность P(>t) того, что время ожидания больше t, в функции от t/tm для различного числа выводов п при поступающей нагрузке А, отнесенной к числу выводов п, равной 0,75 Эрл, полной доступности и случайной нагрузке первого рода

иаоборот, при малых значениях интенсивпости поступающей нагрузки, как и вероятность ожидания, весьма мало.

В рассмотренном выше примере предполагалось, что вызовы обслуживаются в порядке их поступления (первым поступил - первым обслужен). Это допущение оказывает влияние на распре-. деление вероятностей времени ожидания. Однако до тех пор, пока «ожидаемая длительность занятия не учитывается, вероятность ожидания и среднее время ожидания не зависят от дисциплины очереди. Это справедливо как для случайной нитрузии второго рода, так и для пуаоооноюского процесса.

Влияние дисциплины очереди, прежде всего, "проявляется при рассеянии времени ожидания. Для времени ожидания в качестве крайних случаев удобно было рассматривать постоянное и экопо-ненциальио распределенное время ожидания. Для дисциплины очереди роль тких случаев играют обслуживание в порядке поступления вызовов и обслуживание на основе случайного выбора из очереди (случайность при этом означает, что если вывод освобождается, то каждый из ожидающих вызовов может быть выбран с одинаковой вероятностью). Случайный выбор приводит к тому, что время ожидания рассеивается сильнее, чем при обслуживании вызовов в порядке их поступления. Вероятность превышения для малых значений времени ожидания становится меньше, а для больших - больше [6.19].

Другая дисциплина очереди может быть связана с еще большим рассеянием времени ожидания; предельным случаем является обслуживание в порядке, противоположном поступлению вызовов (пришел последним - обслужен первым).

Для систем с ожиданием, имеющих один вывод, справедливы приведенные выше соотношения при п=1; кроме того, следует отметить ещ.е некоторые весьма .общие свойства. Так, вероятность Р{>0)=А независимо от распределения длительности занятия и от дисциплины очереди предполагает, что в дисциплине очереди не учитывается ожидаемая в каждом случае длительность занятия и что интервалы между вызовами распределены экспоненциально. Напротив, вероятность превышения зависит как от распределения длительности занятия, так и от дисциплины очереди.

При тех же предположениях от дисциплины шереди не зависят также среднее число ожидающих вызовов и их среднее время ожидания. Распределение длительности занятия .влияет на эти средние значения лишь постольку, поскольку они ведут к различным значениям рассеяния а-т длительности занятия:

i -/ + {От/иг " 2(1 Л) •

При одинаковых средних значениях длительности занятия и равной интенсивности поступающей нагрузки среднее время ожи-246

Дания получается наименьшим в случае постоянной длительности занятия (от=0); при экспонеициальном распределении (от=т> время ожидания вдвое больше (рис. 6.15).

Рис. 6.15. Среднее время ожидания t*ui всех вызовов, отнесенное к средней длительности занятия tm в зависимости от интенсивности поступающей нагрузки А при экспоненциальном распределении интервалов между вызовами и одном выводе для разных значений рассеяния а™

длительности занятия: СтНт =

=0 - постоянная длительность занятия; а-тНт = 1 - экспоненциально распределенная длительность занятия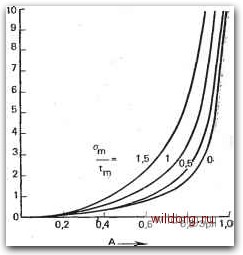

6.2.3.2. СИСТЕМЫ С ОЖИДАНИЕМ С НЕПРЕРЫВАЮЩИМИ ПРИОРИТЕТАМИ

Присвоение ориоритетов отражает особую дисциплину очереди для всего процесса, поэтому приведенные выше соотношения в данном случае также справедливы, если при присвоении .приоритетов нс исходить из ожидаемой длительности занятия. В дальнейшем специально предполагается, что длительность занятия при различных приоритетах характеризуется одним и тем же распределением. Это условие касается систем, у которых на выводах одинаковым способом обрабатываются все вызовы независимо от их приоритета. Примером может служить коммутация с запоминанием для абонентов, сообщения которых обслуживаются в первую очередь, хотя по строению заголовка и длительности они не отличаются от прочих. Кроме того, вызовы, поступающие с тем или иным приоритетом, должны быть распределены .экспоненциально.

Для той доли Л) общей интенсивности поступающей нагрузки, которая обслуживается с наивысшим приоритетом, вероятность ожидания по-прежнему такая же, как .и для общей интенсивности поступающей нагрузки, поскольку уже имеющееся занятие не прерывается. Но время ожидания для ожидающих вызовов меньше, а именно его распределение .совпадает с распределением, которое