вместо g(nT) в (4.5) и (4.6), получаем, что сигнал ,„ j Sinn t/T - .

а его спектр

C{io) = Td, I (О К л/Г. (4.8))

Функции g(t) и G((o) представлены на рис. 4.7. Характеристика G(-со) I на этом рисунке не показана, поскольку G(-(й) = = IG (ш) I. Выражением вида (4.8) описывается передаточная функция идеального фильтра нижних частот. Его амплитудно-частотная характеристика имеет прямоугольную форму (см. рис. 4.76), а фаза и ГВЗ согласно (4.6) изменяются с частотой линейно или постоянны.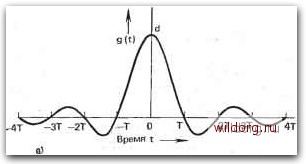

!G(f)

6) Частота f-

Рис. 4.7. Характеристики импульсов, удовлетворяющих первому условию Найквиста: ,. .4,!

а) временная диаграмма сигнала g(t); б) модуль спектра \G(f)\

Таким образом, сигнал (4.7) соответствует реакции идеального •фильтра нижних частот, но лишь при условии, что на вход его подан бесконечно узкий прямоугольный импульс, так называемый импульс Дирака, спектр которого постоянен во всей области частот от -оо до +00 [4.2, 6*]. Если же на вход поступают другие

Вне заданной полосы спектр О(м)=0. Данное условие подразумевается €ез особых оговорок и в дальнейшем.

импульсы, то их спектр следует учитывать в (4.8). Это справедливо и для дальнейшего изложения.

Независимо от сказанного выше реализация сигналов, удовлетворяющих первому условию Найквиста, встречает трудности, так как сигналы, спектр которых сосредоточен в ограниченной полосе частот, имеют длительность во времени от /--оо до оо. Такие, сигналы .не могут появиться иа приеме, поскольку в силу принципа причинности требуют появления сигнала на передаче в момент t=i-оо. Столь же нереальна, в принципе, и интерпретация G{a) в форме (4.6) как частотной характеристики некоторого фильтра, в частности, потому, что функция вида (4.7) нереализуема, а к фильтру предъявляется условие G(c))=0 при ш>я/Г.

Даже если бы импульс в форме функции sinx/x (4.7) был бы реализуем, его нельзя было бы использовать, поскольку он потребовал бы очень точного соблюдения моментов отсчета. При самом незначительном их отклонении ряд для возникающих при этом измененных отсчетов не сходится, т. е. они дают столь большую» межсимвольную интерференцию, что характеристические значения становятся ошибочными. Тогда при любой последовательности импульсов вида sinx/x восстановление информации невозможно. Несмотря на это, такой импульс используют притеоретическо.м анализе для оценки предельных значений.

В дальнейшем рассматриваются только импульсы, которые реализуемы, по крайней мере, приближенно [4.5]. Рассматриваемые импульсы идеализированы, т. е. длятся от оо до оо, как и элементарный импульс вида sinx/x. Однако, как будет рассмотрено в этом разделе, они могут быть ограничены конечным интервалом путем замены точного спектра приближенным.

В результате сглаживания прямоугольной формы спектра по косинусоидальному закону (Roll-Off) получается сигнал, который, как и элементарный импульс sinx/x (4.7), удовлетворяет первому условию Найквиста [4.6]. Спектр вместо прямоугольной приобретает форму

G((o) =

Td для а)<-5-(1-г).

(4.9)

l-sin--((o-)] для (l-r)<(o<-f(l+r),

показанную на рис. 4.8а.

В равенстве (4.9) коэффициент сглаживания г задается в пределах 0</-1, так что спектр может быть максимум на 100% шире полосы Найквиста. [Для г=0 справедливо (4.8)]. Новый сигнал, хотя и удовлетворяет первому условию Найквиста, однако уже не определяется однозначно своими отсчетами g(tiT), поскольку его спектр, вопреки требованию теоремы отсчетов, выходит за 108

пределы полосы Найквиста. Из (4.4) и (4.9) получаем для сигна-- л а выражение

sin (п t/T) cos(nt/T)

git)-

(4.10)

ntfT l - (4r?/T?)t?

Эти сигналы используются в качестве первичных сигналов в системах передачи с частично подавленной боковой полосой и в

rG(f)l 2

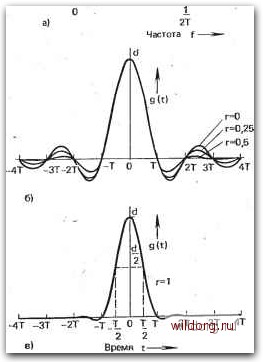Рис. 4.8. Изменение сигнала g(t) при косинусоидальном сглаживании его спектра G(f):

а) модуль спектра G(f); б) сигнал g{t), удовлетворяющий только первому условию Найквиста; в) сигнал g(t), удовлетворяющий первому и второму условиям Найквиста