в соответствии с (2.6) теперь для пары событий (Xj, у) можно определить информацию

»"--;-"«-(7s;r75k))-"+<- „

(2.13)

Это вытекает из того, что совместная вероятность р(Хг, у) пары событий, Xi, ук, может быть представлена как произведение вероятности события Xi на вычисленную с учетом его появления условную вероятность р{ук/хг) события ук.

Порядок следования событий Xi и у можно изменить:

h ft

так как ту же совместную вероятность p{Xi, ук) можно представить в виде произведения вероятности р(г/ь) появления на приеме символа уь-на вероятность р{Хг1ук) того, что был передан символ

Хг, при условии, ЧТО ПрИНЯТ ft.

Количествам информации (2.13) и (2.14) соответствуют математические ожидания информации, т. е. совместная энтропия

Н{Х, У) = Я(Х) + Я(Г/Х) (2.15)

Н{Х, Y) = H{Y) + H{X/Y).

(2.16)

Условные энтропии H{X/Y) и H{Y/X) выражают степень «развязки» полей событий (X, рх) и (Y, ру). На рис. 2.6 это изображается по Схоутену [2.18] в виде двух пересекающихся кругов, причем левый круг представляет Н{Х), правый -Я(У), а жирно окантованная общая площадь - совместную энтропию Я(Х, У).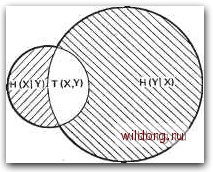

Рис. 2.6. Диаграмма подразделения совместной энтропии Н(Х. Y): обведенная жирной линией общая площадь - совместная энтропия Н(Х, Y), левый круг -энтропия Н(Х), правый круг - энтропия H(Y)

При жесткой связи обоих полей событий (идеальная, свободная от шумов передача) оба круга одинаково велики и совпадают друг с другом, так что заштрихованные площади Я(Х/У) и Я(УД) исчезают. Если, напротив, оба поля события полностью развязаны (на-

пример, из-за разрыва линии связи), то оба круга на рис. 2.6 располагаются отдельно друг от друга, т. е.

HiXlY) = H{X). Я(т) = Я(У), (2.17)

Н{Х, ¥) = Н{Х) + Н(У). (2.18)

В общем случае круги накладываются друг на друга так, что имеется общая часть Т(Х, Y) (канал передачи с шумами).

Составляющие совместной энтропии имеют следующие названия и значение (рис. 2.6 к 2.7): Ц{Х, Y) ~ потерянная часть посланной информации, которая не

достигает приемника; она на- Ненадежность Энтропия

зывается ненадежностью ка- " " нала*; H(Y/X) - та часть h(xY) H(Yx) воспринимаемой приемником информации, которая не имеет отношения к переданной у ,

информации; она называется

иррелевантной информацией н(х)- t(x,Y)-или энтропией илума. Часть

H(Y)-

ИНформацИИ, поступившей на переданная информация

ВХОД канала связи, которая до- „ „ „

, „ Рис. 2.7. Передача информации по настигает приемника, „алу (представление по Е. Р.

Бергеру)

Т{Х, Y)H(X)H{XfY)H(Y)~-H{Y/X) (2.19)

выражает количество переданной полезной информации**. Среднее количество информации, проходящее по каналу в секунду, называют скоростью передачи информации, W (единица измерения - бит/с). Она зависит от свойств канала и источника, однако при допущении всех возможных способов кодирования входного сигнала можно устранить зависимость от свойств источника и получить максимальное значение скорости передачи информации Чтах- Оно называется пропускной способностью канала С и зависит от свойств канала.

К. Э. Шеннон показал, что ненадежность канала И при наличии шума можно сделать сКоль угодно малой за счет надлежащего кодирования, если скорость поступления информации на вход канала не превышает его пропускной способности.

Очень интересно сравнение пропускной способности каналов различных типов, которое было проведено X. Марко [2.19]. Рассмотрим с этой целью следующую модель канала связи для пере-

* В оригинале Aquivokation - неопределенность. (Прим. ред.).

** Ее называют также взаимной информацией входа и выхода. В ориги-=нале для этой величины введен специальный термин «синэнтропия», не получивший распространения в отечественной литературе. (Прим. ред.).

дачи двоичных сигналов (рис. 2.8). Синхронный двоичный канал с интервалом отсчетов Т содержит двухпозиционный канал* с ми-. нимальной длительностью элемента Тагп Т, а последний, в свок> очередь, включает в себя непрерывный канал с ограниченной полосой пропускания В, в котором сигнал подвергается действию шу-

Тактовый генератор

i] гер I

Модулятор

-Фильтр-

Помехи

Тактовый генератор

Канал связи

" "1 Демоду- Триг-

• I Непрерывный канал j

с ограниченной полосой -Двухпозиционный канал -

Двоичный канал

Рис. 2.8. Модель канала связи для передачи двоичных сигналов

ма, характеризующемуся определенным отнощением сигнал/шум {S/\N). Это может привести в двухпозиционном канале к краевому искажению At/T**, а в двоичном канале - к явкоторой ошибке в бите с вероятностью Ре.

В непрерывном канале пропускная способность Со, умноженная на длительность элемента Т=1 (2В), есть, согласно Шеннону [2.4],

GoTlogVl+S/N, (2.20)

а для двоичного канала с вероятностью ошибки в бите ре справедлива соответствующая формула

C,r=l-S(A); 0<S(p,)<l, (2.21)

где S(p) -функция Шеннона из (2.12). Выражение для пропускной способности CiT (где T-Tnin) двухпозиционного канала при передаче по нему сигнала широтно-импульсной модуляции (ШИМ) получено Марко Г2.19]. На рис. 2.9 представлены графики зависимости пропускной способности непрерывного, двоичного и двухпозиционного каналов от отношения SjN (в логарифмических единицах) . Как видно, двоичный канал (вследствие присущей ему избыточности по отношению к передаче сигнала) имеет пропускную способность СгТ, которая в широких пределах не зависит от отноше-

* Для указанного участка канала в отечественной литературе такой термин малоупотребителен. (Прим. ред.).

** Это не единственное последствие действия шума в непрерывном канале (Прим. ред.).