которого ввод свободен до .нового вызова, стремится к нулю. Интенсивности поступающей и потерянной нагрузок тогда произвольно велики. Средняя нагрузка стремится к числу вьгоодов, т. е. в

предельном случае все выводы постоянно заняты. С другой стороны, вероятность потерь обращается в нуль лишь тогда, когда больше нет поступающей нагрузки (если не учитывать случай, когда число вводов не превышает числа выводов).

0,20 г

0.15 -

6 0.10

0,05 -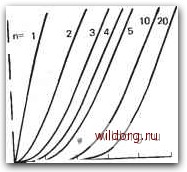

0 2 0,4 0,6 0,8 Эрл 1.0 А

Рис. 6.13. Вероятность потерь В в функции от интенсивности поступающей нагрузки, отнесенной к числу выводов п, при полной доступности (k=n) и случайной нагрузке первого рода для различных значении л

Полная доступность в одноступенчатой схеме с т вводами и п выводами означает, что всего имеется тп точек коммутации. Последнее справедливо и для временной коммутации, например, в соответствии с рис. 6.5: в т моментов времени имеется по п точек пространственной коммутации. Однако затраты на регистр соединений растут пропорционально числу линий, которые он обслуживает, следовательно, для схемы рис. 6.5 - пропорционально числу вводов. Но поскольку адреса выводов представлены не

кодом I ] , а двоичным кодом, то при удвоении числа выводов

адресная кодовая комбинация удлиняется только на один бит. Поэтому при временной коммутации можно применять одноступенчатые полнодоступные схемы и при большом количестве подключенных линий.

6.2.2.2. НЕПОЛНОДОСТУПНЫЕ СХЕМЫ

При неполной доступности вероятность потерь возрастает, так как к потерям ведут не только те вызовы, которые поступают, когда все выводы заняты, но и те, которые поступают, когда свободные выводы недоступны. Это можно особенно просто сформулировать математически при случайной нагрузке первого рода.

При доступности k, где k<n, для вероятности потерь справедливо выражеиие

где Cj - вероятность того, что состояние / (/ выводов занято, т. е. п-/ выводов свободно) не может быть достигнуто ни одним выводом (вероятность блокировки). Вероятности Cj и Bj при этом складываются из отдельных вероятностей различных возможностей того, что / выводов занято. При полной доступности величина Cj обращается в нуль, таким образом получается приведенное выще соотношение:

Простейшая одноступенчатая неполнодоступная схема является результатом подразделения вводов или соответственно поступающей .напрузии и вьшодов на подгруппы с полной доступностью. При подразделении на z подгрупп требуется в общей сложности

Z--• - точек коммутации. Однако вероятность потерь сильно

возрастает, так как не происходит выравнивания нагрузки между подгруппами. На рис. 6.13 приведены графики вероятностей потерь для больших пучков линий [6.16]; результат действия подразделения, например, на две одинаковые подгруппы, виден из сравнения вероятности потерь для п и п/2 выводов. При общей интенсивности поступающей нагрузки, равной 6 Эрл, неполном пучке из.десяти отводящих линий (0,6 Эрл на линию) вероятность потерь составляет около А%, а при подразделении на два пучка по пять линий - около 11%.

В схемах со смешивающими ступенями (см. рис. 6.10) вероятность потерь меньше, чем при подразделениии на подгруппы. Однако расчет вероятностей состояний, а тем самым и вероятностей потерь составляет в данном случае, как и для других неполно-доступных схем, особую проблему из-за большого числа различных состояний.

6.2.3. СИСТЕМЫ с ОЖИДАНИЕМ

Определяющим показателем для оценки системы с ожиданием [6.1?, 6.18] является вероятность того, что вызов должен ожидать обслуживания в течение времени, большего t, т. е. вероятность превышения P(>i) (в частности, вероятность Р(>0) того, что вызов вообще должен ожидать обслуживания). Другим важным показателем часто служит среднее время ожидания для всех вызовов i*w или же среднее время ожидания обслуживания для ожидающих вызовов iw

Два последних показателя связаны между собой соотношением

С=ш(>0)+о{1-Р(>0)]=/,р(>0),

поскольку среднее время ожидаиия для всех вызовов складывается из указанных в формуле частей времени ожидания для ожидающих и иеожидающих вызовов.

Размеры очереди определяются количеством ожидающих обслуживания вызовов. Его среднее значение w, само по себе, конечно, не достаточное для определения размеров очереди, рассчитывается по среднему числу вызовов, поступающих в единицу времени, Altm, и среднему времени ожидания всех вызовов (поскольку все вызовы могут ожидать обслуживания сколь угодно долго и, следовательно, ни время ожидания, ни длина очереди не ограничены),

W = е: •

tm .

В таком виде соотношение справедливо для совокупности всех вызовов; если применяются приоритеты, то соответствующее соотношение справе,рливо для каждого приоритета /:

В дальнейшем будем исходить из того, что интенсивность поступающей нагрузки не зависит от состояния и интервалы между вызовами распределены по экспоненциальному закону. Рассмотрим вначале схемы с п вьгоодами, а затем такие же схемы с одним ;выводом. В системах с ожиданием они играют большую роль, так как в общем случае доступ к центральным коммутационным устройствам осуществляется через систему с ожиданием. По той же причине особое значение имеет случай, когда длительность занятия постоянна. Системы с ожиданием, имеющие ограниченную доступность, напротив, здесь не рассматриваются, т. е. в дальнейшем предполагается полная доступность.-

6.2.3.1. СИСТЕМЫ С ОЖИДАНИЕМ БЕЗ ПРИОРИТЕТОВ

Используя тот же подход, что и при описании систем с потерями, рассмотрим систему со многими выводами, которая имеет случайную нагрузку. Пусть имеется только одна очередь и нет приоритетов. Предположим, что очередь и время ожидания не ограничены, а вызовы обрабатываются в порядке их поступления.-Процесс является стационар.ным только в том случае, если вызовов поступает в среднем меньше, чем может быгь обслужено с помощью п выводов, т. е. А должно быть меньше п.

Вероятность ожидания определяется вероятностью того, что вызов поступил и должен ждать, деленной на вероятность того, -что вызов вообще поступает в тот же отрезок времени. При случайном обмене первого рода, используя вероятности состояний, получаем выражение 244