тематическим методам поиска минимума функции многих переменных. Наиболее иввестный из них - градиентный метод. При использовании этого метода определяются частные производные минимизируемой фунции по каждой переменной. При расчете жор-ректора с функцией ошибок F получают, таким 01браеом, выражения dFjdcv. ОбраЗОванный из них градиент функщии

указывает направление наиболее сильного возрастания функции F. где Av - единичный вектор v-й координатной оси в п-мерном пространстве. Бели при изменении функции двигаться в направле-. нии, обратном градиенту, то обеспечивается наиболее сильное уменьшение функции. Тогда при достаточно малых Шагах в ходе некоторого итерационного процесса функция будет все более и более Приближаться к искомому минимуму. Наконец, когда при выбранном шаге минимум будет пройден, процесс настройки будет колебаться около точки минимума, причем с тем большим отклонением, чем больше шаг. Бели шаг выбрать слишком большим, то первоначальная погрешность снижается лишь незначительно, если же, папротив, использовать очень малый Шаг, то для достижения минимума потребуется очень МНого итераций. Между этими нежелательными крайними случаями имеется некоторое оптимальное значение шага, которое зависит от вида минимизируемой функции. У корректора шаг настройки зависит от искажений, т. е. в конечном счете от характеристик канала связи. При этом, как правило, оптимальное значение шага для разных итераций различно.

Однако при настройке корректора с помощью такого рода итерационного процесса кроме правильного .выбора шага должно быть выполнено и еще одно условие: выбранная функция ошибок. Например среднеквадратическое отклонение от требуемого значения, должна содержать в себе достаточную информацию о характеристиках корректируемого канала связи. Это отнюдь не подразумевается само Собой. Так, именно при передаче данных могут появляться такие особые последовательности битов, которые дают лишь одну или неонолько спектральных линий. Отмеченное обстоятельство Приводит к тому, что корректор хотя и очень хорошо настраивается на передаваемый текст, однако при изменении текста должен сначала найти новую, возможно, совсем другую настройку, а до этого мож-ет иметь место погрешность. В некоторых случаях по указанной .причине процесс настройки корректора может расходиться. Чтобы устранить отмеченный недостаток, принимают дополнительные мары к тому, чтобы, по крайней мере, при начальной настройке корректора спектральные линии были равномерно распределены по всей полосе передачи и лежали близко

друг от другй. с этой целью .передаются либо отдельные сильно удаленные друг от друга импульсы, либо псевдослучайный текст. Чтобы избежать перестройки корректора из-за особенностей передаваемой последовательности также и ,при нормальной передаче, передаваемые .данные часто дополнительно тгреобразуют в передатчике в псевдослучайную последовательность с помощью скремблера, а в приемнике вновь вОсстанавливают их с помощью дескремблера. Такое преобразование данных в псевдослучайную последовательность, как .правило, необходимо также .и для того, чтобы сигнал данных содержал в себе достаточную информацию о фазе несущей и тактового .синхросигнала (см. разд. 4.4.1).

Необходимо .обсудить и еще один важный вопрос: как могут быть .определены величины, требуемые для оптимальной настройки коэффициентов корректора.

Разумеется, оувет зависит от выбранного типа корректора. Детальный анализ для корректора, при .котором минимизируется максимальное искажение, можно найти в [6.24]. Настройка коэффициентов Cv для м.инимизации .среднеквадратической погрешности рассматривается в [6.26] применительно к трансверсально-му фильтру. При этом оказывается, что частные праизводные, необходимые для настройки корректора, можно непосредственно получить как взаимную корреляцию между сигналами Sv (t) на отводах трансверсального фильтра и отклонением s(t)-Si(t):

=р [s{t)~Si(t)]sAt)dt,

(6.4)

Выход Требуемое значение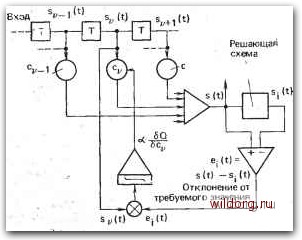

Рис. S.22. Настройка коэффициентов с у трансверсального корректирующего

фильтра по среднеквадратическому отклонению значений рассматриваемых отсчетов от требуемых

где Si(t) - требуемое (неискаженное) значение сигнала; s(t} - значение сигнала на выходе корректора. Используя Эти нроизвод-ные, для упомянутой ныше перестройки коэффициентов в направлении, обратном градиенту, новые .коэффициенты следует определять по старым в соответствии с формулой

dQ 5с„

(5.5)

10"

10"

10"

Реализация описанной настройки коэффициентов показана на рис. 5.22. В Соответствии с (5.4) вначале по сигналу s(t) на выходе корректора с помощью .решающей схемы определяется требуемое значение Si(t), а затем с/помощью дифференциального усилителя - .отклонение .от требуемого значения ei(t)==s(t)-Si(t), Эта ош.ибка умножается на сигнал sv С v-ro отвода линии задержки. Так как интегрирование в пределах от -=1-оо до оо, как это требует (5.4), естественно, невыполнимо, то частная производная определяется приближенно по достаточно большому чи- .,о-слу точек отсчета /:

dQ 2 щг\ - •

После умножения на некоторую величину .а согласно (5.5) получаются сигналы настройки коэффициентов Чтобы реализация была простой, величина .а обычно выбирается постоянной. Оценка ее значения приведена, например, в [5.26]. Как показано в [5.27, 5.28], путем надлежащего выбора а при соответствующих условиях можно существенно сократить время настройки корректора.

Влияние различных значений « на процесс настройки трансверсального корректирующего фильтра показано на рис. 5.23. При слишком малом а оптимальная настройка достигается лишь за длительное время, а слишком большое зна-

О 200 400 600

Число передаваемых битов -

80а.

Рис. 5.23. Сходимость настройки трансверсального корректирующего фильтра при различных значениях коэффициента шага а (см. рис. 5.22). Период использованной квазислучайной двоичной последовательности -

150 битов, время интегрирования -

50 отсчетов