получается, если имеется только нагрузка с интенсивностью Ау [6.11]. В соответствии с этим среднее время ожидания .

f i+(Cm/tmr , l-A

lull - m ТГГ, Т\ - w ~ ~

2(1-l-Ai

сокращается по сравнению Со средним временем ожидания tw для всего процесса. Аналогичные соотнощения справедливы и для той доли поступающей нагрузки, которая обслуживается с низшим приоритетом. При незначительной общей нагрузке присвоение приоритетов 1не приводит к заметным последствиям, а при интенсивной нагрузке его результаты, наоборот, очень заметны; прежде всего; среднее -время ожидания для ожидающих вызовов со всеми приоритетами, кроме самых низких, такж.е остается конечным, если общая нагрузка стремится к п. Для пояснения на рис. 6.16 показано среднее время ожидания всех вызовов пр.и их разделении поровну по трем приоритетам. Соответствующие соотношения справедливы и для систем с более чем одним гвыводом [6.20].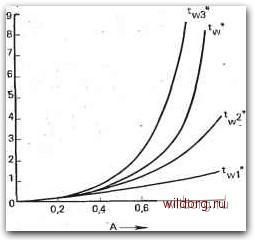

0,8 Эрл 1.0

Рис. 6.16. Среднее время ожидания t*„ всех вызовов и среднее время ожидания всех вызовов с одним из трех приоритетов t*wi, t*w3 при отрицательном экспоненциальном распределении вероятности интервалов между вызовами, равномерном распределении интенсивности поступающей нагрузки по приоритетам и одном выводе (время ожидания отнесено к о=- tm(l+amlPm), где tm - средняя длительность занятия, От - рассеяние длительности занятия)

6:2.3.3. ДРУГИЕ СИСТЕМЫ С ВОЗМОЖНОСТЬЮ ОЖИДАНИЯ

. Принятое выше допущение, что очередь не ограничена, т. е. со-держит по меньшей мере столько же imcct, сколько имеется выводов, выполняется не всегда. В системе с ограниченной возможно-248

стью ожидания вероятность потери меньше, чем в чистой системе с потерями, а среднее времяожидания короче, чем в системе с ожиданием без ограничений.

Если в системе с различными приоритетами важно уменьшить не только среднее время ожидания для ожидающих вызовов с высокими нриоритетами, но и вероятность ожидания, то занятия, имеющие более низкие приоритеты, должны прерываться. Вызовы с наивысшими нриоритетами тогда обслуживаются так, как будто бы существует только эта часть нагрузки. Вероятность ожидания лри этом снижается, и распределение ожидания внутри указанного приоритета определяется только значениями длительности занятия для вызовов с этим приоритетом.

С помощью некоторых других мероприятий можно минимизировать среднее время ожидания для всех вызовов, например, так, чтобы вызовы с кратчайшей ожидаемой длительностью занятия обслуживались с наивысшим приоритетам.

6.2.4. ИЗМЕРЕНИЯ НАГРУЗКИ . -

6.2.4.1. ИЗМЕРЕНИЯ ПАРАМЕТРОВ

в предыдущих разделах вопросы теории телетрафика рассматривались с использованием определенных распределений. Если считать вид функции распределения известным, например утверждать, что имеет место экспоненциальное распределение, то тогда задачи измерения нагрузки состоят в том, чтобы получить параметры ее распределения (например, средний интервал между вызовами в часы наибольшей нагрузки), которые должны быть определены путем измерений [6.21]. При этом для некоторых сетей передачи данных ;может оказаться, что нет ярко выраженной концентрации нагрузки по времени [6.22].

Измврения параметров необходимы, прежде всего, для того, чтобы можно было выявить длительные изменения нагрузки и своевременно приспособить устройства коммутации к изменившимся требованиям. От таких длительных изменений следует отличать кратковременные изменения, которые наблюдаются, например, в то время, когда происходит переход от меньшей нагрузки к большей или наоборот [6.23]. Анализ этих переходов с точки зрения теории телетрафика составляет особую проблему, на которой останавливаться не будем.

6.2.4.2. ОПРЕДЕЛЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

Однако, как правило, нельзя исходить из того, что вид функции распределения известен. Поэтому желательно, чтобы и сам вид функции распределения можно было определить путем изме-

рений. На практике ограпичиваются определением некоторых ее моментов: среднего значения, рассеяния и моментов высших порядков. Моментом -го порядка случайной величины х, центрированной по отношению к а, называют математическое ожидание величины [х-а).

После этого неизвестное распределение можно описать с помощью другого распределения, имеющего те же моменты.

6.2.4.3. ОБЪЕМ ИЗМЕРЕНИИ

При неизвестном распределении существенную- роль играет объем измерений, необходимых для того, чтобы достаточно точно определить паретры распределения. Под точностью понимаются два понятия - доверительный интервал и коэффициент доверия (доверительная вероятность). Доверительный интервал указывает, насколько полученные из измерений значения отклоняются от истинного значения. Коэффициент доверия показывает, с какой вероятностью величина попадает в доверительный интервал. На основе определенного объема измерений можно установить некоторый узкий доверительный интервал с меньшим коэффициентом доверия и более широкий доверительный интервал с более высоким коэффициентом доверия.

В качестве примера приведем полученные в [6.24] .формулы для измерений длительности занятия при случайной нагрузке первого рода. Согласно [6.24] истинное среднее значение tm лежит в доверительном интервале:

где tm рассчитано по данным измерений п занятий; S - требуемый коэффициент доверия и Я(5) -значение, полученное по нормальному распределению величины S. Найденная зависимость показана на рис. 6.17. Чтобы при одинаковых коэффициентах доверия иметь одинаковые доверительные интервалы, для распределения длительности занятия с более сильным рассеянием требуется выполнить больше измерений, чем для распределения с меньшим рассеянием.

6.2.4.4. ПРОВЕДЕНИЕ ИЗМЕРЕНИИ

Одна из простых возможностей измерения параметров заключается в том, чтобы непрерывно контролировать состояние занятости соответствующих устройств и на основе этого определять интересующие нас величины. При этом необходимо, чтобы имелось